Let's recall that one of the primary functions of any structure is to resist any load it may experience. Ideally, when that happens, we expect it to remain as is - same position and same shape; however, that is not the case.
One important thing to note about forces is that it reshapes and deflects objects from their original place. For example, when we sit on a bench, it may bend. Sometimes we may feel this depression when we sit down. When you walk along a concrete beam, it deflects but is imperceptible.
The object's actual shape after imposing loads on it is its deflected shape.
What is Compatibility?
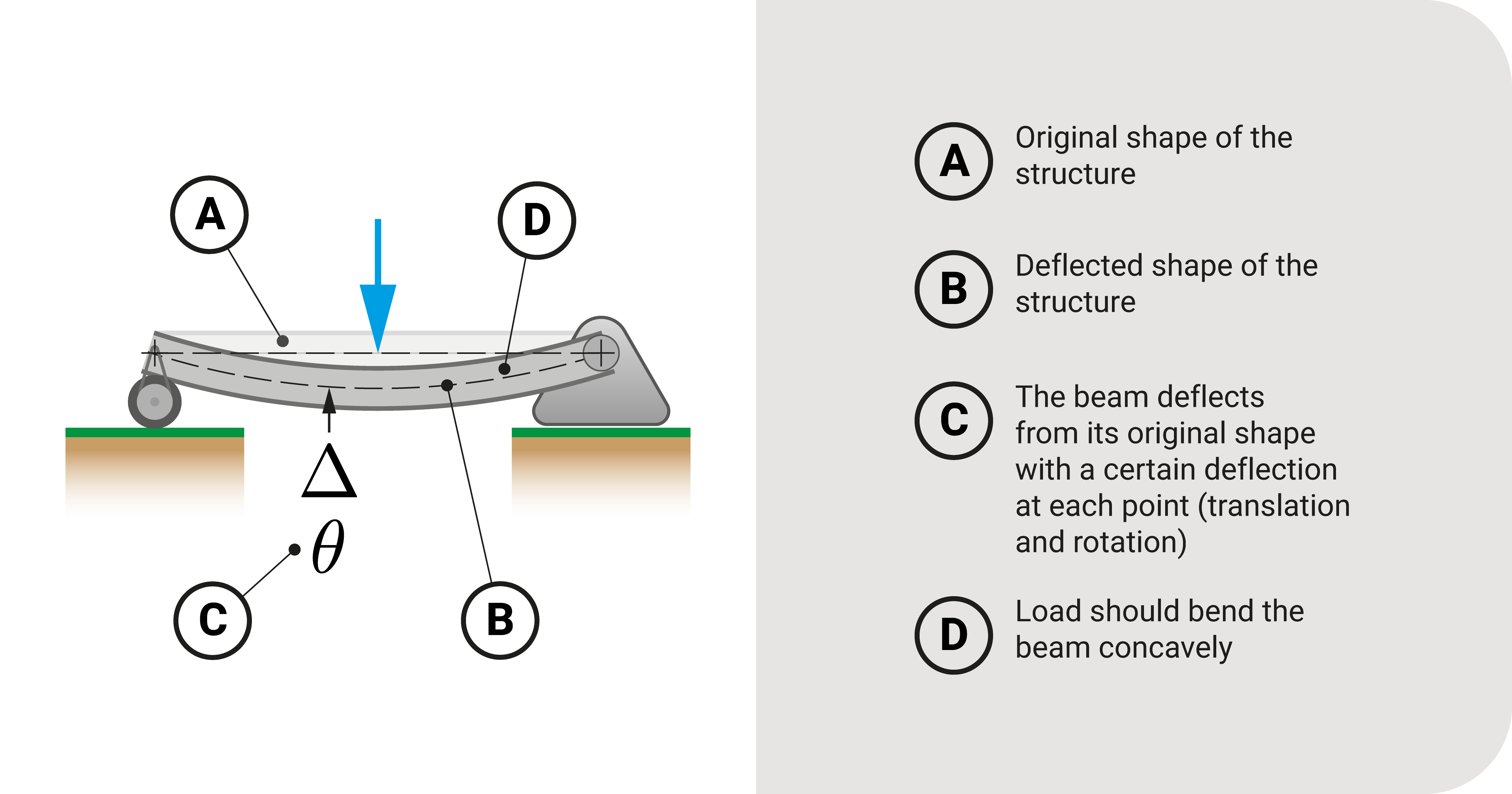
Compatibility refers to the balance between the structure's deflected shape and the structural loads imposed on it. Usually, what we're analyzing here is the relationship between the applied loads and the deflected shape of the object - we're making sure these two connect well.
Let's move to a structural example. If we impose a downward vertical force on a beam, we expect it to bend concavely. We don't expect its deflected shape to elongate or twist. The object's shape should change appropriately with the applied force.
Compatibility Conditions
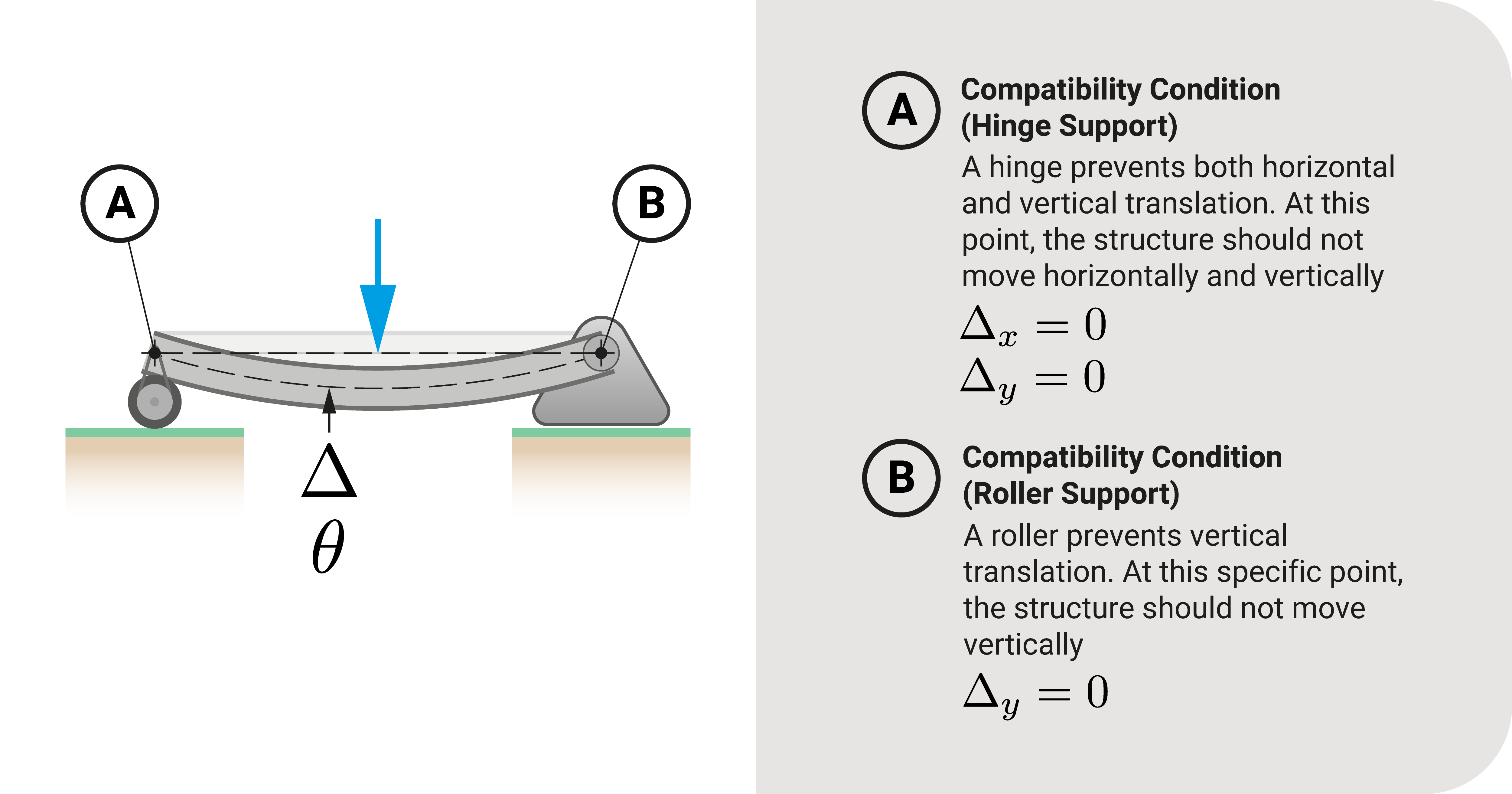
We use this concept to find the known movements for specific points of the structure. From there, we derive what we call compatibility conditions which are boundary conditions.
Let's illustrate this by investigating roller supports. Recall that these carry the structure's loads and tell us about movement restraints. A roller can move along the surface or rotate; however, it cannot move perpendicularly to the supporting plane. That restricted movement along the vertical is the condition we are interested in taking note of.
Where Do We Use Compatibility Conditions?
We'll explore using these conditions as we go along the course. As a taste, we create these conditions and use them in the solution of:
- Deflections. We use it as boundary conditions that help us know the movement of a structure at a specific point.
- Statically Indeterminate Structures. When dealing with these structures, these conditions are mandatory! They are the additional equations needed to solve the skeleton.
Summary
The deflected shape on the structure is the actual shape when it's imposed with loads.
Compatibility refers to the balance between the structure's deflected shape and the effect of structural loads imposed on it.
Compatibility conditions are equations that tell us general deflection conditions at specific points of the structure.






