Remembering the different trigonometric identities can be a difficult task.
One way to make things easier is to create a tool to help us recall it. This post will discuss the hexagon trigonometric tool we'll use to identify multiple identities.
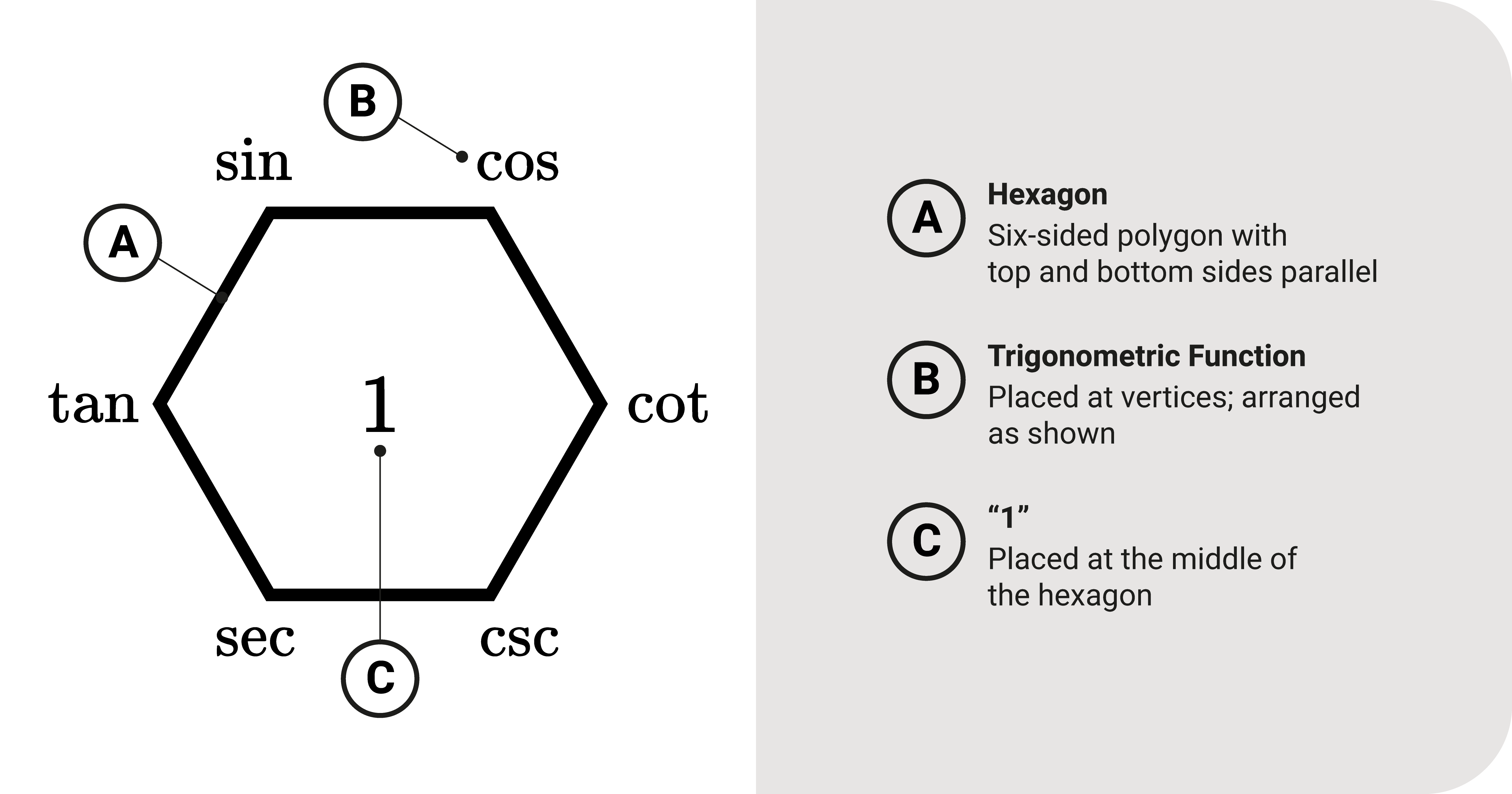
Hexagon Mnemonic
To create the tool, follow these steps:
- First, draw a hexagon. The bottom edge of it must be perpendicular to you.
- Next, starting from the top-left vertex, label each vertex around the hexagon clockwise with the functions in order: sine, cosine, tangent, cosecant, secant, and cotangent.
- Then, place inside the polygon the value one.
Voila! We just created the hexagon drawing - it should be similar to the figure below:
Now that we have this tool, we can derive different identities
Reciprocal Identity
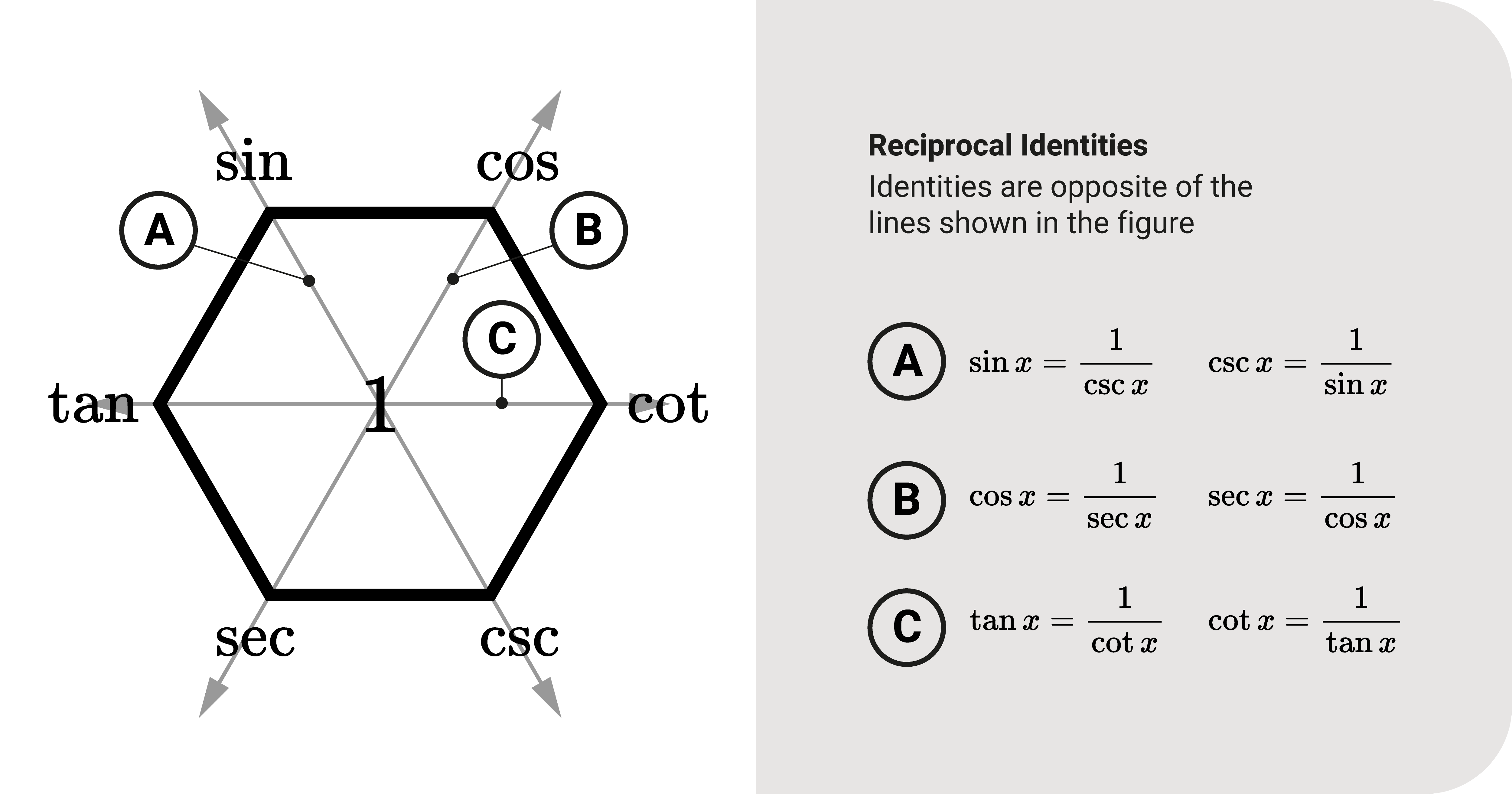
We first start with the simplest one: the reciprocal identity. As you recall, there are six trigonometric functions.
One key observation is that the first three functions, \(\sin\), \(\cos\), and \(\tan\), are the reciprocals of the other three, \(\csc\), \(\sec\), and \(\cot\). These are what we call reciprocal identities.
Let's go back to our drawing. Where do we see it? Consider a line connecting two directly opposite vertices and investigate the functions along the line. For example, let's use the diagonal connecting \(\sin\theta\), 1, and \(\csc\theta\).
- If you read the line from sine downwards, the identity is \(\sin\theta=\frac{1}{\csc\theta}\)
- If you read the line from cosecant upwards, the identity is \(\csc\theta=\frac{1}{\sin\theta}\)
This example shows how to read said identities: when a line connects two directly opposite vertices, they are reciprocals.
From this, there are only three possible lines: \(\sin-\csc\), \(\cos-\sec\), and \(\tan-\cot\).





