What are the Derivative Tests?

Second Derivative Test

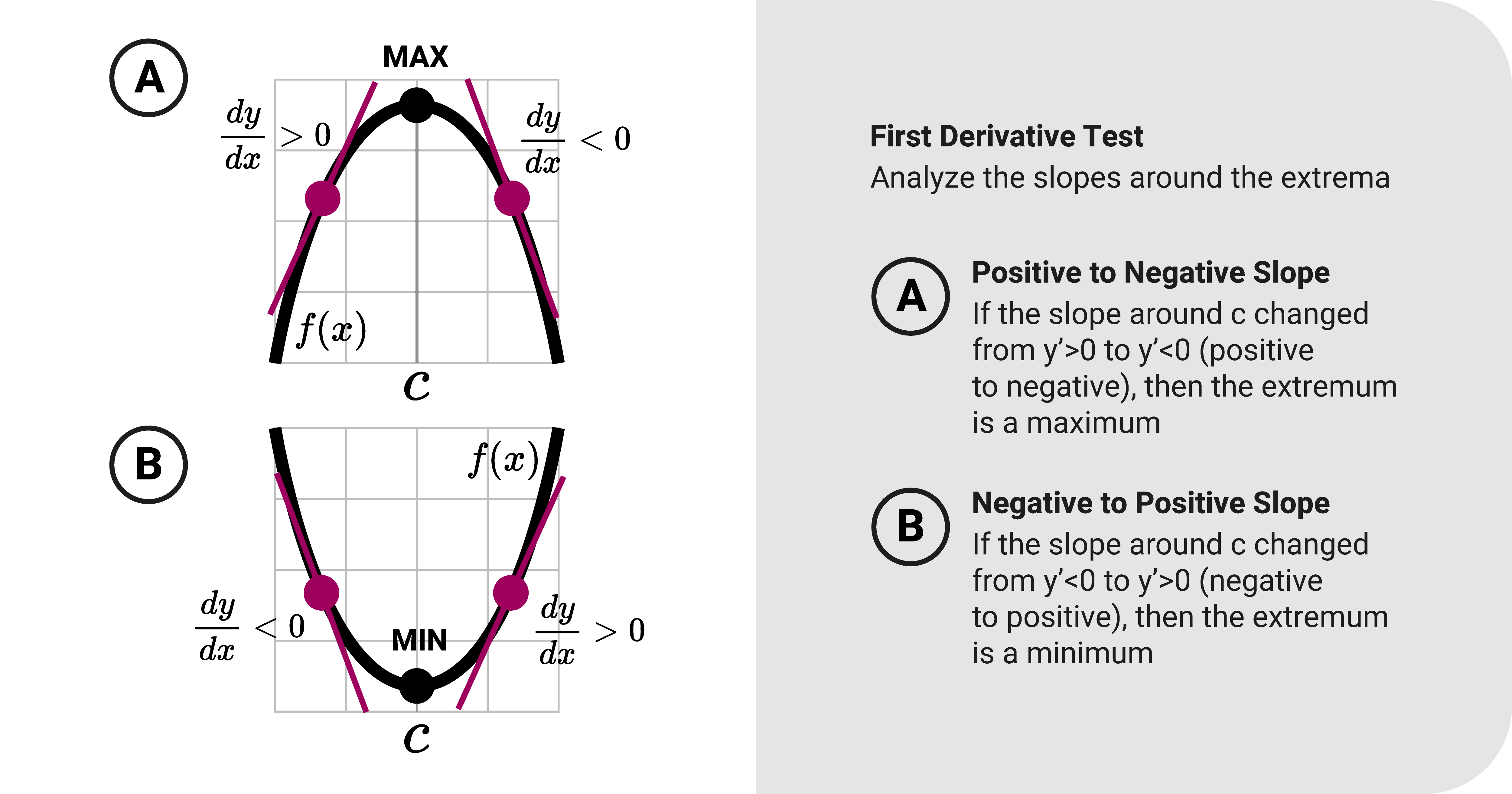
Next, we consider the second derivative test. We use the second derivative to classify an extremum.

Again, consider a function \(f\) and a specific interval. Also, assume there is a critical point, \(c\), so there is an extremum. To check if it is a maximum or minimum:

• If \(y^{\prime \prime}\) is negative (concaving downward) around \(c\), the extremum is a maximum.
• If \(y^{\prime \prime}\) is positive (concaving upward) around \(c\), then the extremum is a minimum.

If the result of the test is zero, the test fails. We must use the first derivative test or other means to classify the extremum.

Summary

We can check if an extremum is a maximum or minimum by performing some tests.

In the first derivative test, the extrema is a maximum if the slope \(y^{\prime}\) around \(c\) changed from positive to negative (function increased then decreased). On the other hand, the extrema is a minimum if the slope \(y^{\prime}\) around \(c\) changed from negative to positive (function decreased then increased).

In the second derivative test, if \(y^{\prime \prime}\) is negative (concaving downward) around \(c\), the extremum is a maximum. Otherwise, if \(y^{\prime \prime}\) is positive (concaving upward) around \(c\), then the extremum is a minimum. If the result of the test is zero, the test fails. We must use the first derivative test or other means to classify the extremum.