Almost every mathematics course will involve the study of functions. But why study it? To put it simply:
It's A Way To Model Phenomena
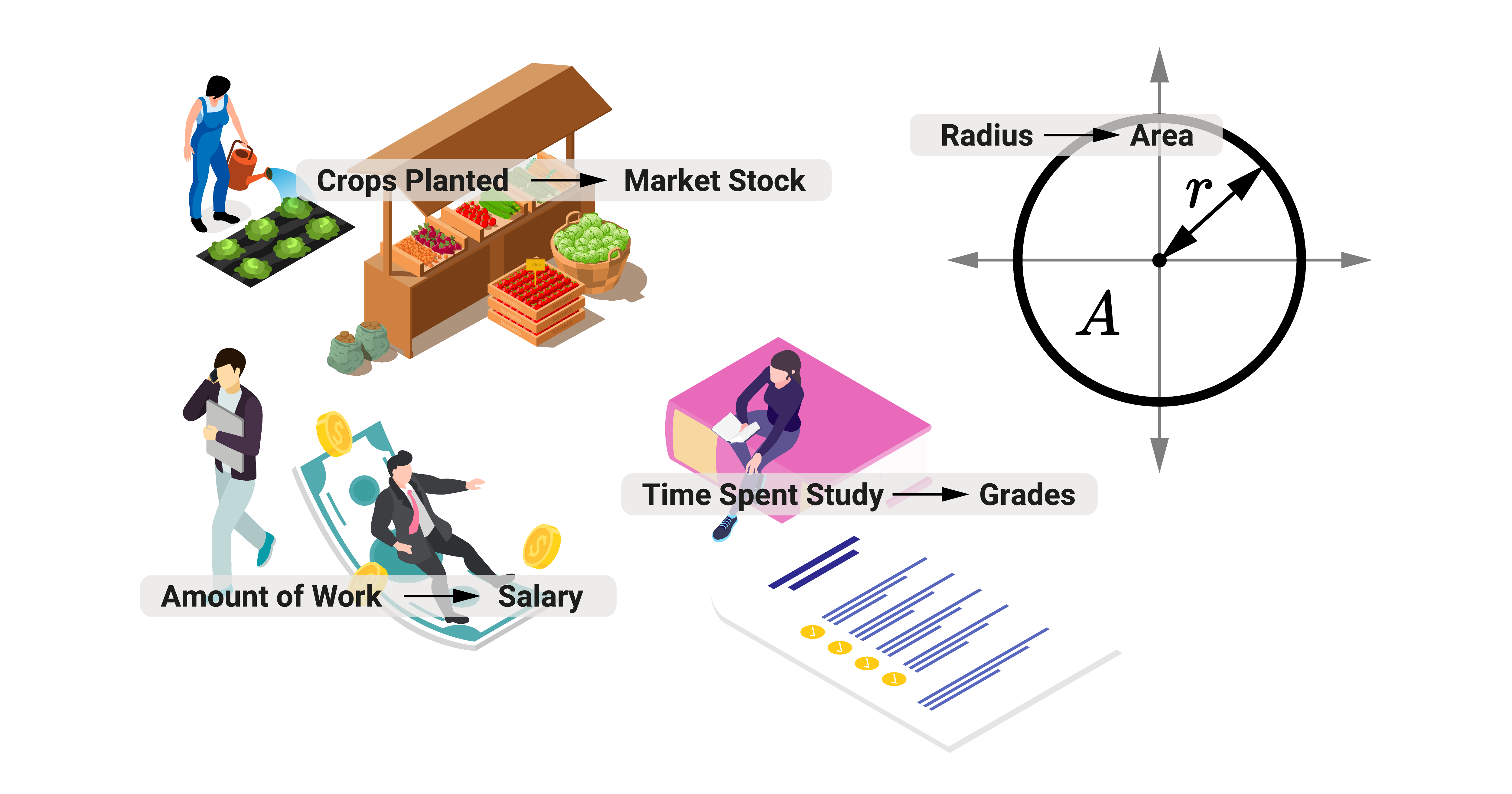
Functions (and relations) can represent most of the world's events. To demonstrate, the following are examples of relationships:
- The money put inside a vending machine and the drink that will come out of it
- The time spent studying and the resulting grades
- The distance traveled by a vehicle to its speed
- The radius of a circle to its area
- The amount of workforce and work accomplished
- The number of hours spent in the office and one's salary
- The number of customers and the sales generated
- The amount of water evaporated and the intensity of the rain
- The amount of sunlight and crop production
The examples above are just a handful of many phenomena we can represent using functions. Once we create these expressions, it can help us analyze, investigate, and predict behavior among these sets. It provides us with a model or a structure that leads us to the next point:
A Tool For Creating Solutions
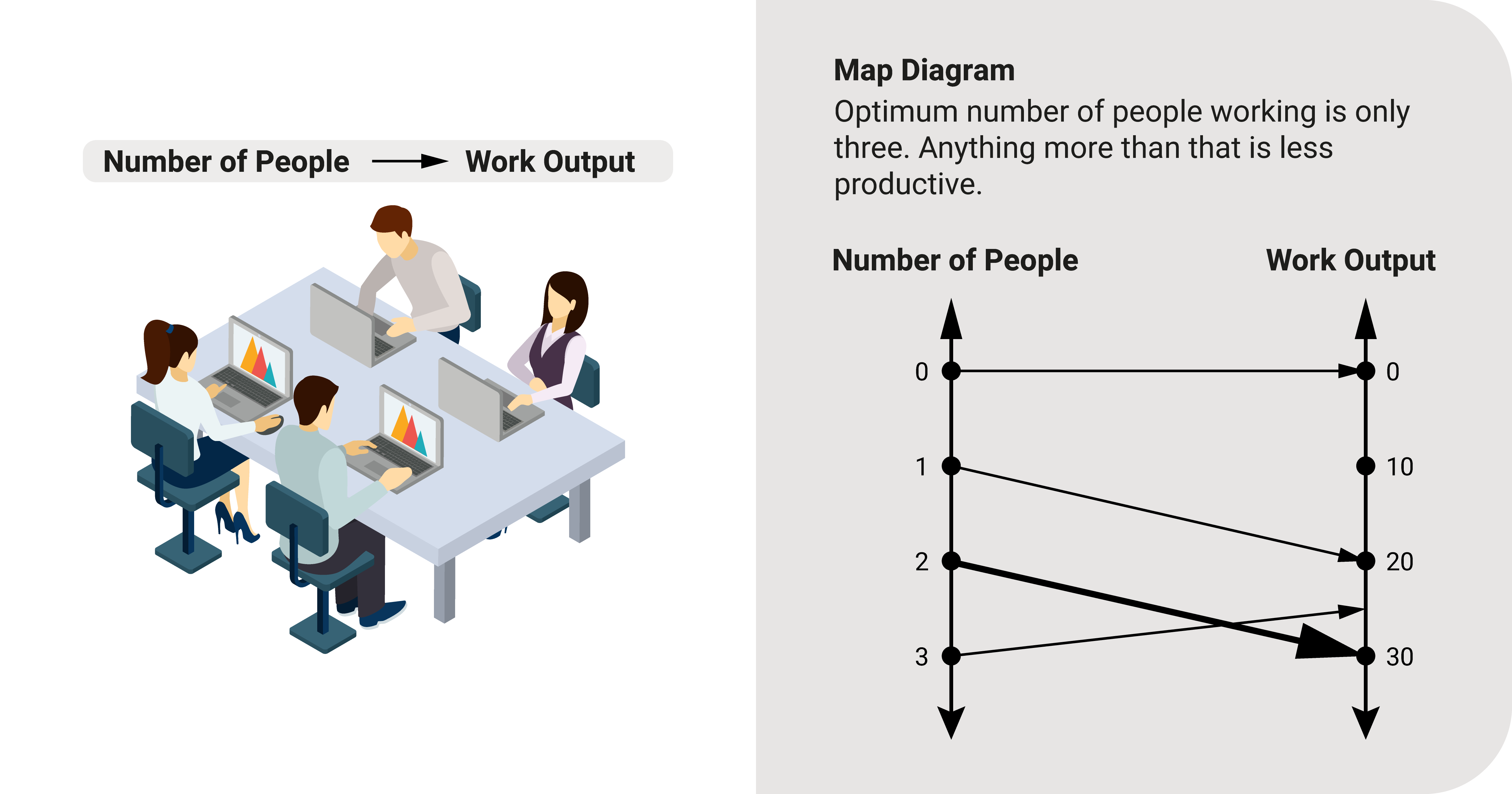
Functions serve as a tool to help us develop solutions, improve products and services, or make logical choices. There are many things we can do with it once we create one. For example:
- When we know the link between hours in the office and work generated, we can find the optimum number of hours to ensure maximum output.
- We can find the right amount of water if we know the link between crop production and watering.
- We can predict sales if we have a relation between sales and the number of customers.
- We will know the optimum number of workers needed to finish a task if we see the connection between the worker and their job.
Some Examples
Let's consider more specific examples of the use of functions:
- In the study of projectile motion, we use two functions to describe the position of the projectile along its trajectory: \(d_x{t}=V_x{t}\) for horizontal and \(d_y{t}=d_o+V_y{t}+g{t^2}\) for vertical distance. We use the variable time \(t\) - domain to get the object's position in both directions. Knowing these functions allows us to accurately predict where it will land and make adjustments when designing cannons and other equipment.
- We can model bacteria growth as an exponential function \(e\). As time \(t\) (domain) goes by, the number of bacteria \(N_B\) (range) grows exponentially: \(N_B=Ce^{rt}\) (the symbols \(C\) and \(r\) are constants). Analyzing how bacteria grows over time helps us how to culture or engineer it.
- Engineers aim to study the behavior of internal forces on objects when subjected to loads. To achieve this, they express internal forces such as axial \(N\), shear \(V\), moment \(M\), and torsion \(T\) in relation to the object's position (x). Engineers specify the domain, which is the position (x) they want to investigate, and the function yields the range, which includes \(N\), \(V\), \(M\), and \(T\). Finding these will help engineers design the appropriate size and shape of the object.
Summary
Functions are a way to represent phenomena.
Functions are tools that help us create solutions.






.png)