Continuing from this example, let's learn how to solve this complex truss using the method of bar conversions.
The solution presented is in SI. The author will update the post soon to reflect English units.
Main Solution
Full Solution
The following section shows how to use the method of bar conversions:
For this method, we will break down the complex truss into two simple structures: a simple truss and a proxy truss. When we add these two structures together, you'll get the bar forces for each complex truss.
Convert to a Simple Truss
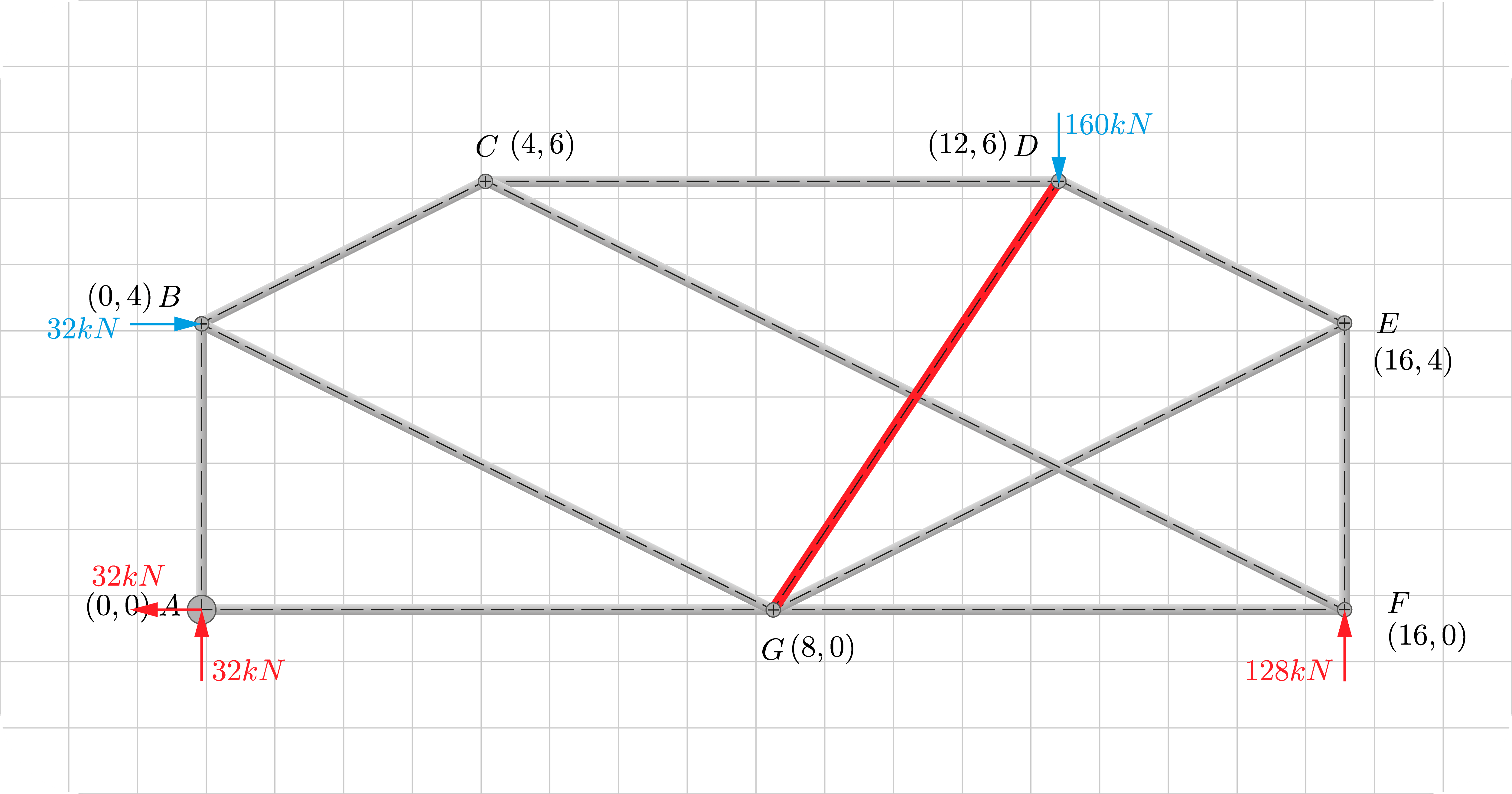
The first step is to convert our complex truss into a simple one by removing any member, say \(AD\); however, in doing so, we made the truss unstable. To reverse that effect, we add another member, say \(DG\). There is no rule on what member to remove or add. Just remember that our goal here is to make our truss simple.
We load this simple truss with the supports and loads like that of our original complex truss. The result is a new structure with the same reactions and loads \(S_p\), serving as an element for the superposition process.
Like any other simple truss, the next step is to thoroughly analyze the reactions and bar forces of this simple truss using the method of joints or sections. It is up to the reader how to solve for such values.
At the end of the analysis, we will have the axial forces of each member summarised in the table shown. Remember that \(AD\) does not exist in this truss, and \(DG\) is a substitute member for stability purposes.






