As an alternative solution to the method of joints, we can use the method of sections to solve for the internal bar forces of a truss structure.
Key Idea: Divide the Truss Into Parts
The method of sections revolves around dividing the truss into two parts by strategically cutting it with a plane. When you cut the truss, you reveal the internal forces of members you would like to solve; afterward, we analyze one or the other part of the truss and solve for these internal bar forces using equilibrium equations. As an analogy, it's like placing a section along the beam to reveal the shear force \(V\) and bending moment \(M\) at a specific point and then analyzing either the left or right part of the beam to solve for \(V\) and \(M\).
General Outline
Strategically Place the Cutting Plane
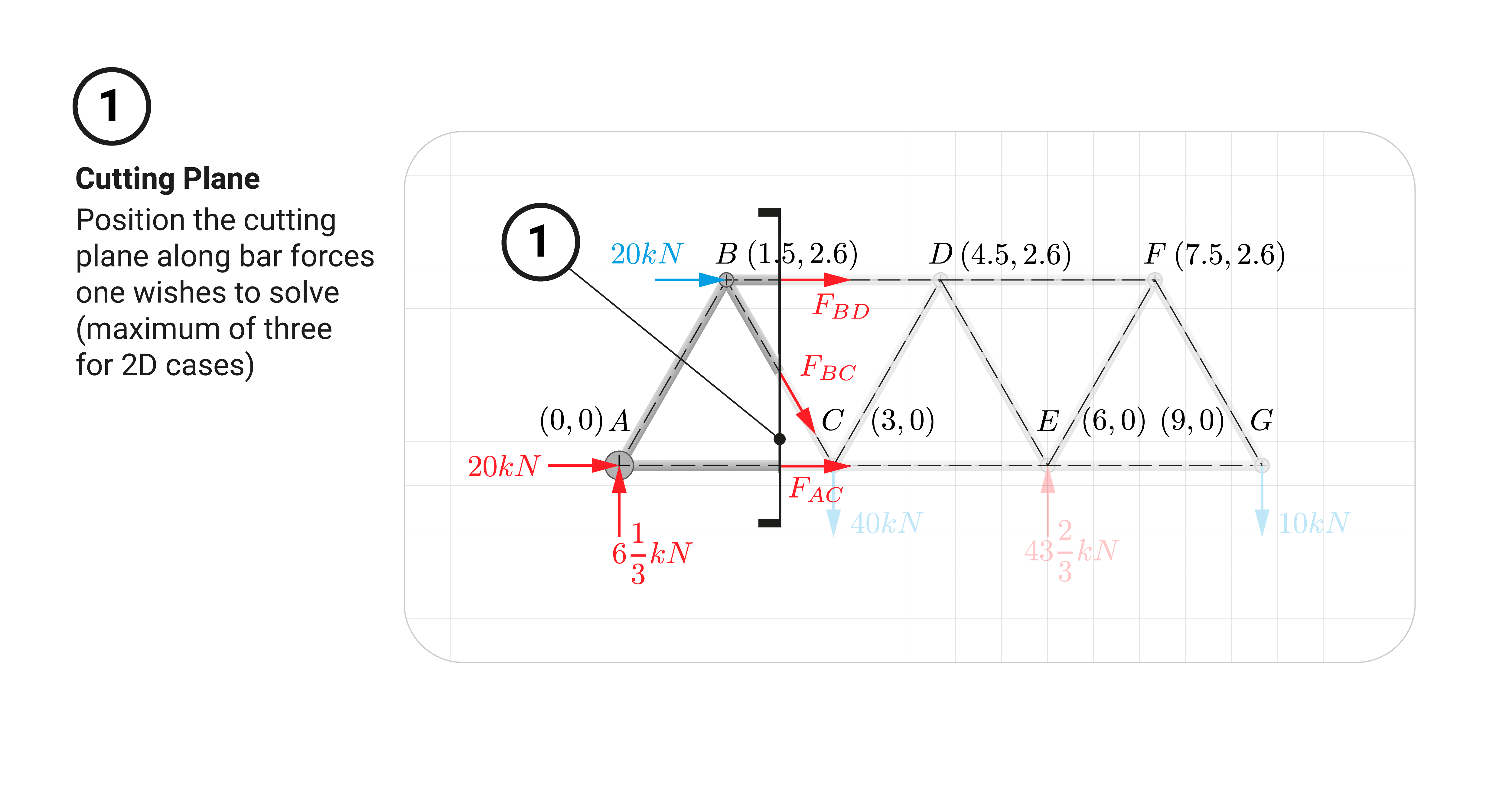
Whenever we use the method of sections, as a general rule, place a cutting plane through a maximum of three members. For 2D trusses, we can only apply three equilibrium equations; hence we can only have a maximum of three unknowns.
When we place a cutting plane that will cut these members, it will divide the truss into two free-body diagrams (FBD). The cut members will have all internal forces exposed (typically assumed tension at the start).
All Parts of the Structure Must Be In Equilibrium
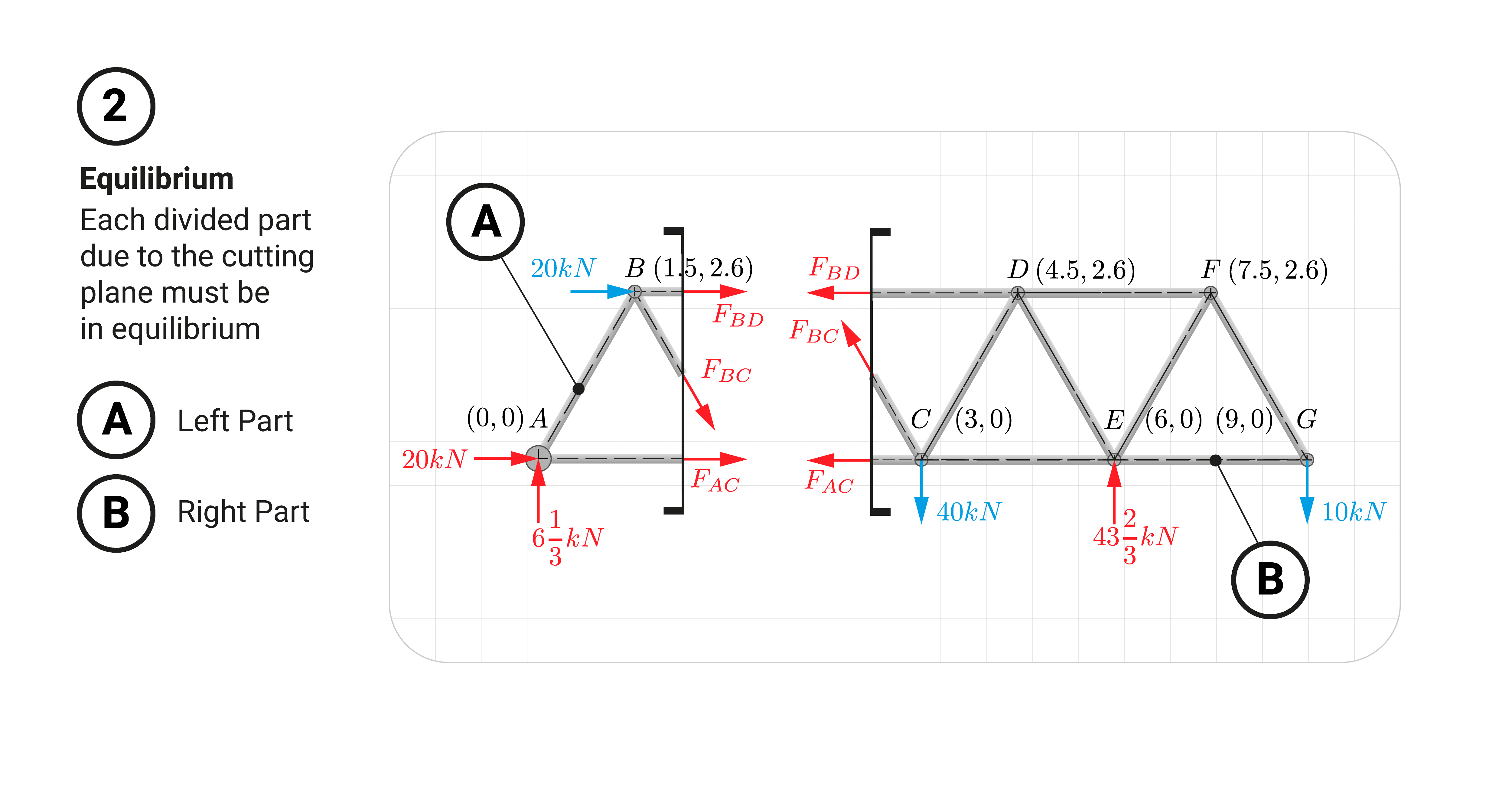
Since we have divided the truss into two parts, we can choose either one or the other part to solve for bar forces.
To solve for the cut forces, remember that this structure must be in equilibrium. It must be true also for the divided parts. We can learn more about this through an example.
Repeat Analysis
When you finally solve the cut bar forces, you can find another section and repeat the process until you've solved every member. Midway, you can switch to the method of joints if you prefer.
Tips
- Again, you can analyze either one part or the other. You can also use the other part as a check to your solution whether your computations are correct.
- When revealing bar forces, it is an excellent strategy to have a uniform assumption in terms of direction to avoid confusion later. Generally, we assume it to be tension (away from the joint).
- Identifying the points of intersection of all bar forces we cut BEFORE proceeding with the equilibrium analysis is a good idea. These points of intersection are usually the best pivot points for all force components when applying the moment equilibrium condition.
- Try to identify points of intersection that will eliminate as many internal forces as possible.
- The method of sections makes it easy to solve for internal forces of horizontal parallel trusses such as the Warren truss (top and bottom chords are parallel). When we apply the equation of equilibrium to one part of the truss and apply the equilibrium condition along the y-axis, you'll only have one unknown since the two chords are parallel with the x-axis.
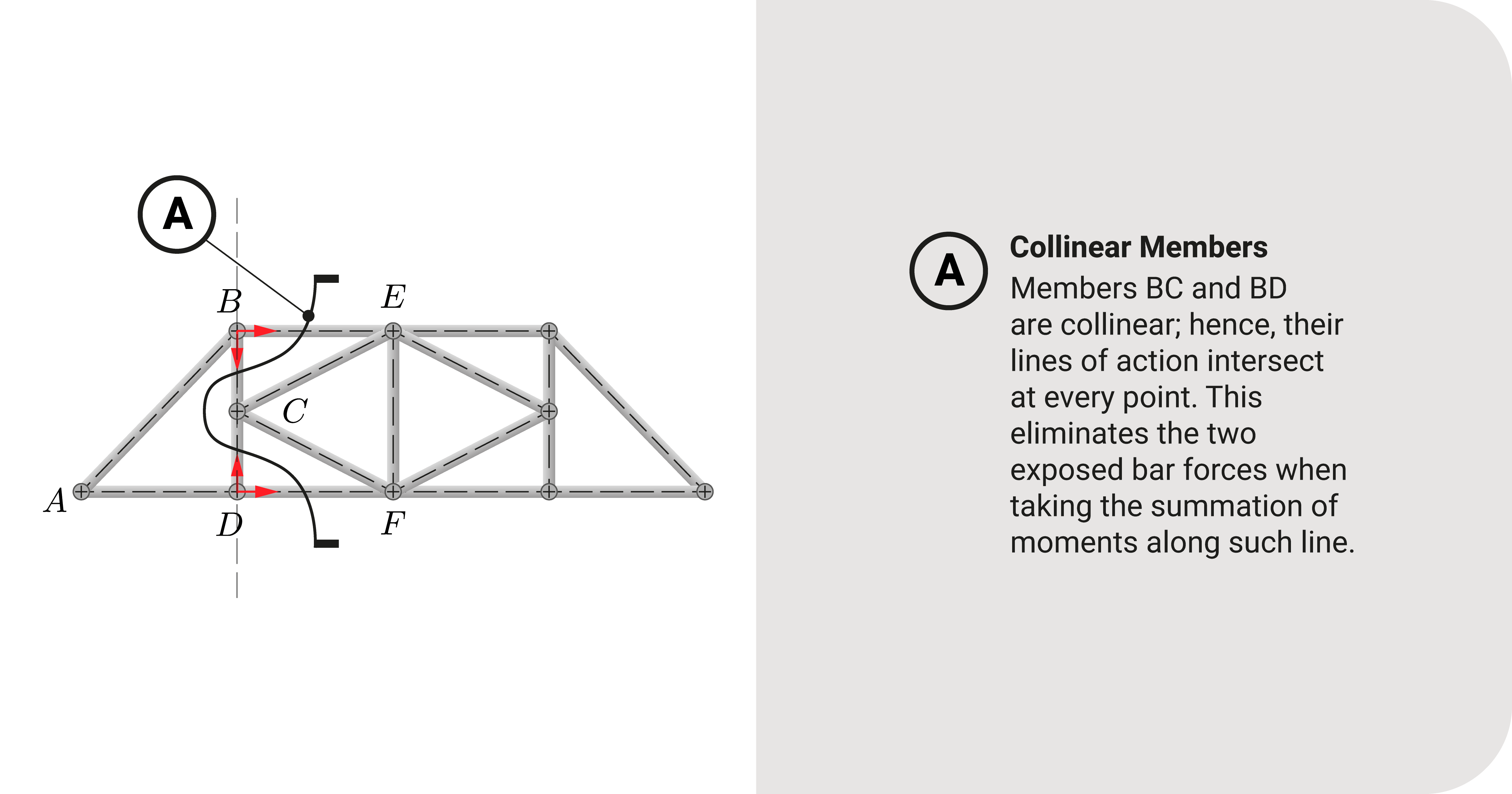
- It is possible to solve for the bar forces of a truss with a section that will cut four or more members because members are concurrent or collinear - an example of this is the K-truss, as shown below. We place a section that will cut four members and apply the moment equilibrium condition with the pivot point at the intersection of the corner left of a panel - you'll notice that these three forces pass through this point; hence, we eliminate three out of four. As a result, you can directly solve for the one unknown force immediately.
Summarise Your Results
After analysis, it is always a good idea to summarise your results using a table.
Application
- Let's illustrate how to use the Method of Sections to solve bar forces for a simple truss.
Summary
Let's summarize:
We can use the method of sections to solve for the internal bar forces of a truss structure.
The method of sections revolves around dividing the truss into two parts by strategically cutting it with a plane. Each division must be in a state of equilibrium.
We first strategically put a cutting plane to expose at most three internal bar forces. Afterward, we choose one part of the divided truss and solve these exposed forces by applying the equilibrium principle.





