We begin our study of fluids with fluid pressure.
Fluid Pressure
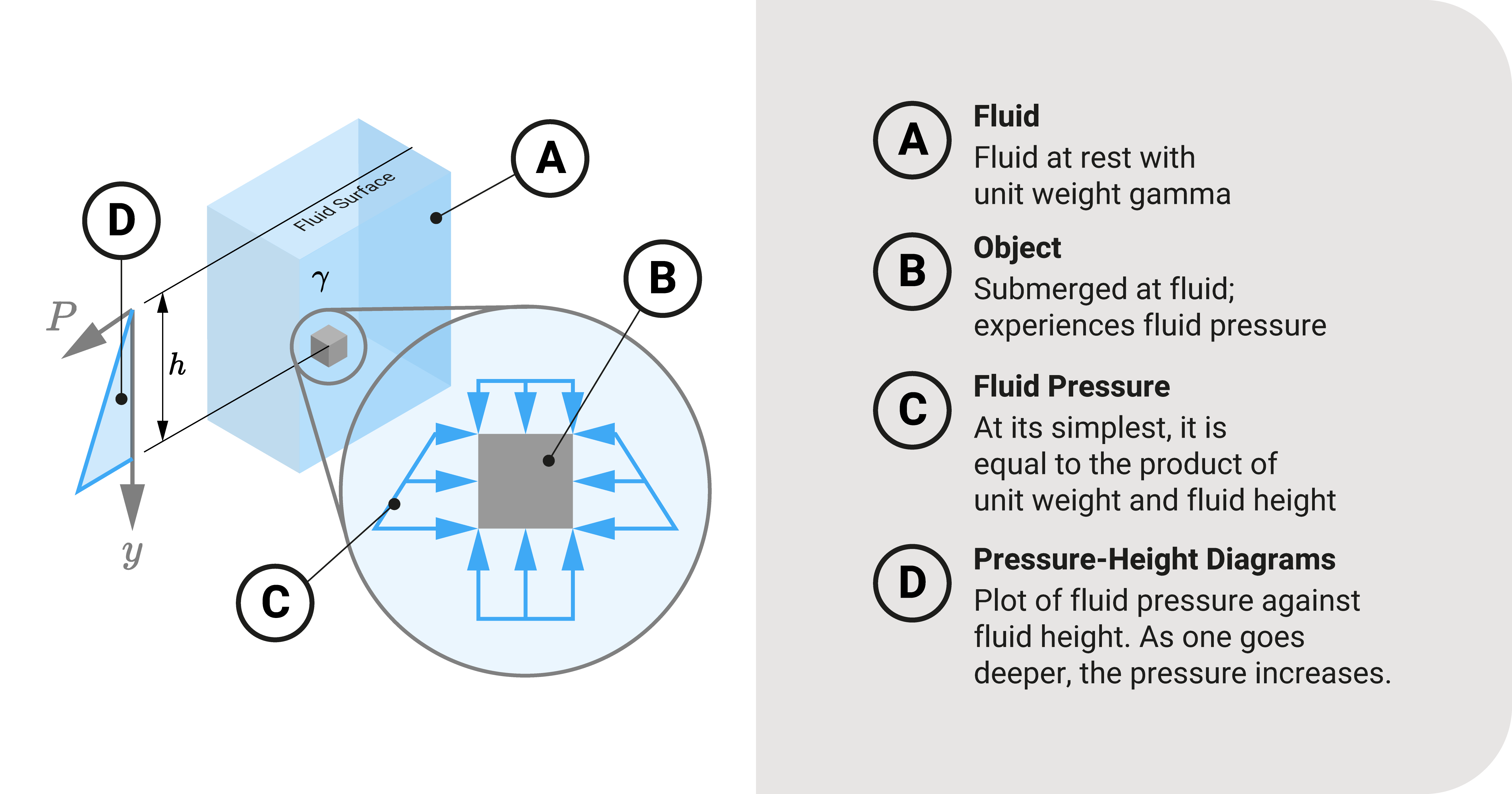
Let's start by defining pressure \(P\). At its most basic, it is a perpendicularly-applied force \(F\) per unit area \(A\):
\(P=\frac{F}{A}\)
Standard units would be Pascal (Pa), pound-force per square inch (psi), atmospheres (atm), or specific manometric units such as (mmHg).
Keen readers will find that this expression is similar to stress because it is the same. We use the term stress for solids and pressure for fluids.
In Fluid Statics, pressure is the unit weight of the fluid \(\gamma\) times height from a reference (usually the surface) \(h\).
\(P=\gamma h\)
Since unit weight \(\gamma\) is the product of density \(\rho\) and acceleration due to gravity \(g\), we have:
\(P=\rho g h\)





