Moment By Parts is another approach to express the internal bending moment of a structure. It is an alternative way of drawing moment diagrams.
This procedure makes our analysis more straightforward. It allows us to compute the area of the moment graph quickly rather than using concepts in integral calculus. In addition, we may need to find the centroid of the moment diagram in specific topics, which may be difficult. Moment By Parts helps us simplify this concern.
Key Idea: Break The Structure into Cantilever Parts, Then Superimpose
This procedure relies on two concepts: (1) cantilever beam patterns and (2) superposition.
The former depends on a solid understanding of the cantilever beam, which we can discover more about in this link. What's important to understand is that there is a fascinating pattern with the beam's moment diagram.
The latter deals with an essential concept in classical analysis. Superposition tells us that a beam can be a sum of similar independent beams.
General Outline
The following is a general outline of how to use moment by parts:
Strategically Cut the Beam Into Parts
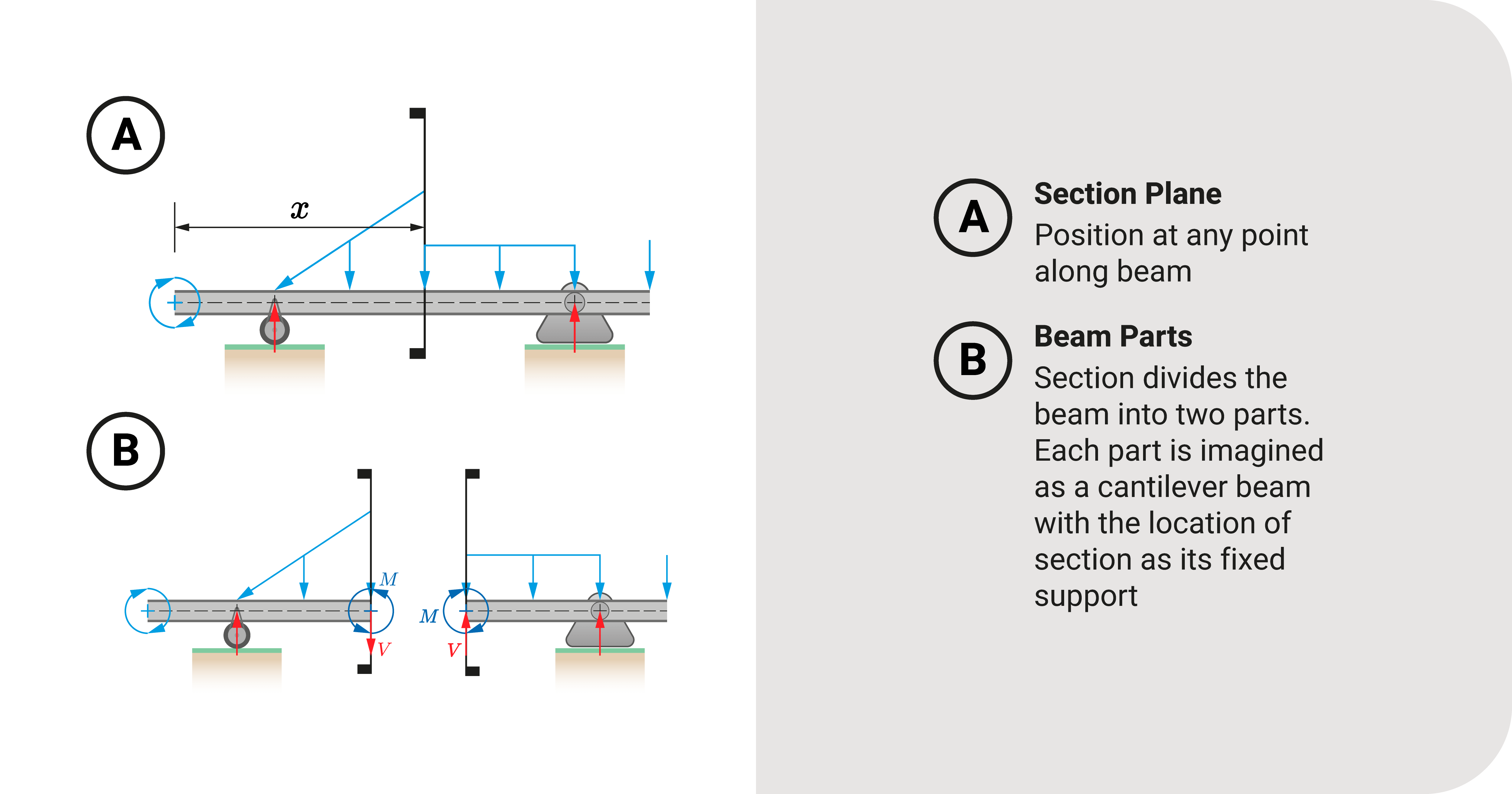
The first step when using the moment diagram by parts is to place a cut section in the beam. When you cut the beam at any point, you'll divide it into the left and right sections. Not only that, you'll reveal its internal shear and moment at the cut point.
With the beam divided, let's shift our perspective of the beam. Consider one division of the beam. If you look closely at this part, it is analogous to a cantilever beam. The unknown shear and moment are like the reactions of the cantilever's fixed-end support. The loads, including its reaction loads, are like the cantilever's external forces. The same is true if you consider the other division.
Another way of thinking about what we did is that we divided the beam into two cantilever beams.









