How to Analyze Deflections Qualitatively?

We can analyze deflection qualitatively - approximate the deflected shape of structures based on the support conditions, internal force analysis, and joints.

WeTheStudy lets you connect ideas

Learn more

We can analyze deflection qualitatively. That is, we can approximate the deflected shape of structures.

This post will explore how to imagine it under flexural loadings. It is a valuable skill, especially if we want rough deflection results or as an aid in the area-moment method.

When approximating the deflected shape, we have to take note of the following:

Supports

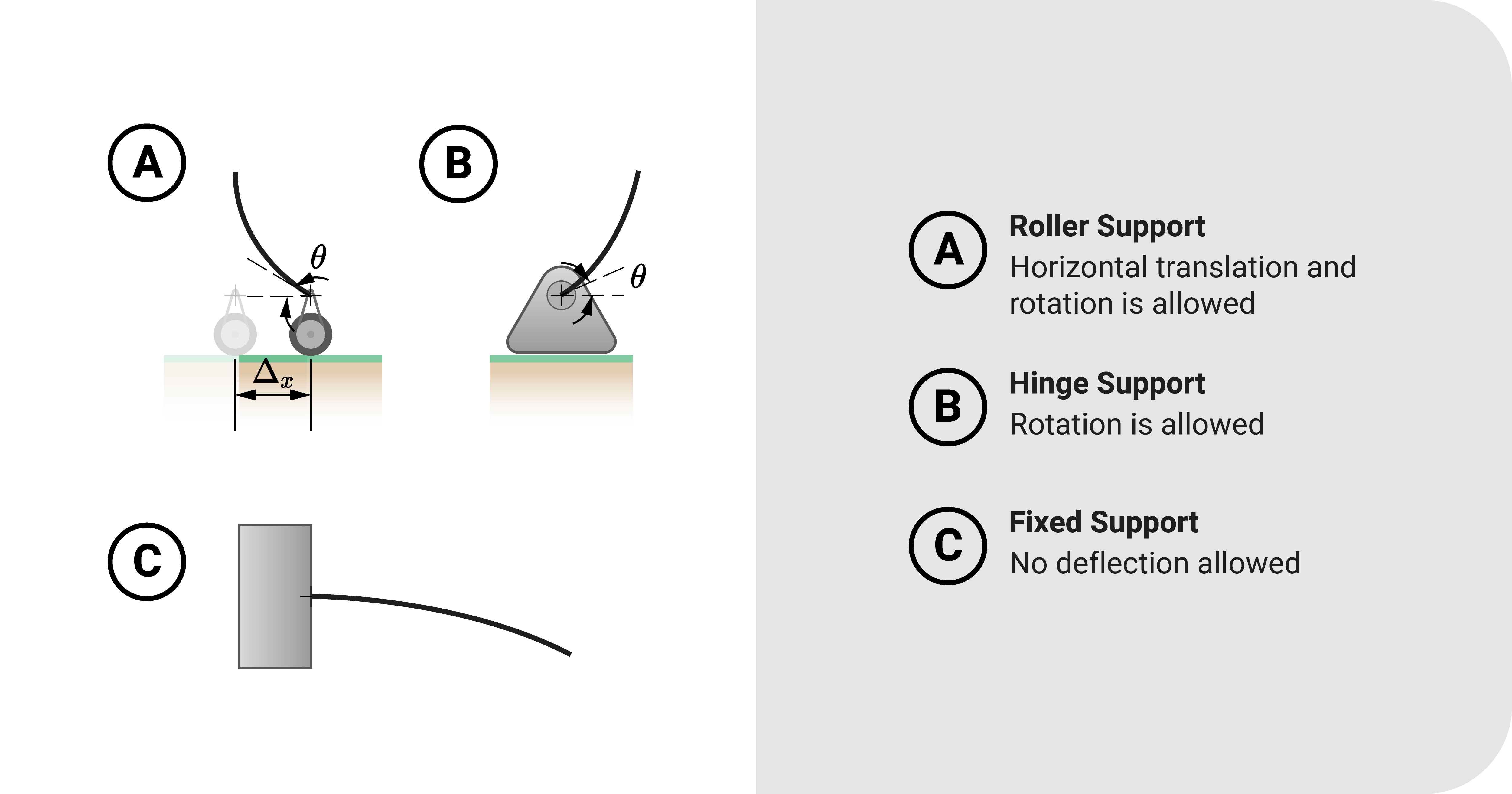
The supports of the structure act as clamps for deflection. For example:

Roller support will allow horizontal translation or rotation but never vertical translation.
A hinged support will never allow translation but will permit rotation.
Fixed support will never allow any form of deflection.

We can discover more of these restrictions here. From these conditions, we can deduce what deflection is like on these supports.

Want to access the remaining content?

You're a Member!

Click to expand on exclusive content

Want to access the remaining content?

Become a Member

When you sign-up and subscribe to WeTheStudy, you’ll get the following benefits:

No ads! (yey!)

Complete access to all articles

Ability to track your progress in the tree

SIGN-UP

Complete Your Checkout

When you complete your account, here are the following benefits:

No ads! (yey!)

Complete access to all articles

Ability to track your progress in the tree

PROCEED CHECKOUT

Member

To approximate the deflection of a flexural member, we must consult its moment diagram. Using the concave upward convention, we can tell if a member will concave upward or downward:

If the member experiences a positive moment, then it concaves upward.
On the other hand, if it is negative, then it concaves downward.
If a member has no moment, then it will not bend.

At points of zero moments, we have a point of inflection - a point in which the curve changes its concavity - from downward to upward or the other way around.

Joints

In addition to supports and members, we can approximate the joint behavior when deflected. We have to consider three things:

Interconnected joints must have the same deformation. If a joint in the frame moved by a certain distance \(\Delta_1\), then the next joint must also move by \(\Delta_1\).
We must follow joint rigidity. For example, if a 90º rigid joint rotates by angle \(\theta\), then after rotation, the joint must still be 90º. If a joint is a pin, then the rigidity is somewhat optional.
Follow equilibrium at joints. All moments acting on it must cancel out.

Summary

Let's summarize:

We can analyze deflection qualitatively. That is, we can approximate the deflected shape of structures.

The supports of the structure act as clamps for deflection.

To approximate the deflection of a flexural member, we must consult its moment diagram.

When approximating joint behavior, we have to consider three things: interconnections, rigidity, and equilibrium.

No ads?

Tree Navigation

See how this article relates to other ideas

Children

No children (yet)

Siblings

What is the Bernoulli-Euler Beam Theory?

Concept

Bernoulli and Euler created theories on how beams behave under the influence of loads. In this post, we'll explore the two fundamental assumptions when analyzing beam deflection.

Parent