After solving the conjugate effects to get the slope and translation, we encounter a tricky question: how do we know the direction of deflection based on the computed conjugate shear and moment? Will said point go up or down? Will that point rotate clockwise or counterclockwise?
The answer will depend on the convention when one analyzes a beam. For a concave upward direction:
- The left section of the beam concaves upward if the shear is downward and the moment is counterclockwise.
- The right section of the beam concaves upward if the shear is upward and the moment is clockwise.
From these, we can conclude the following:
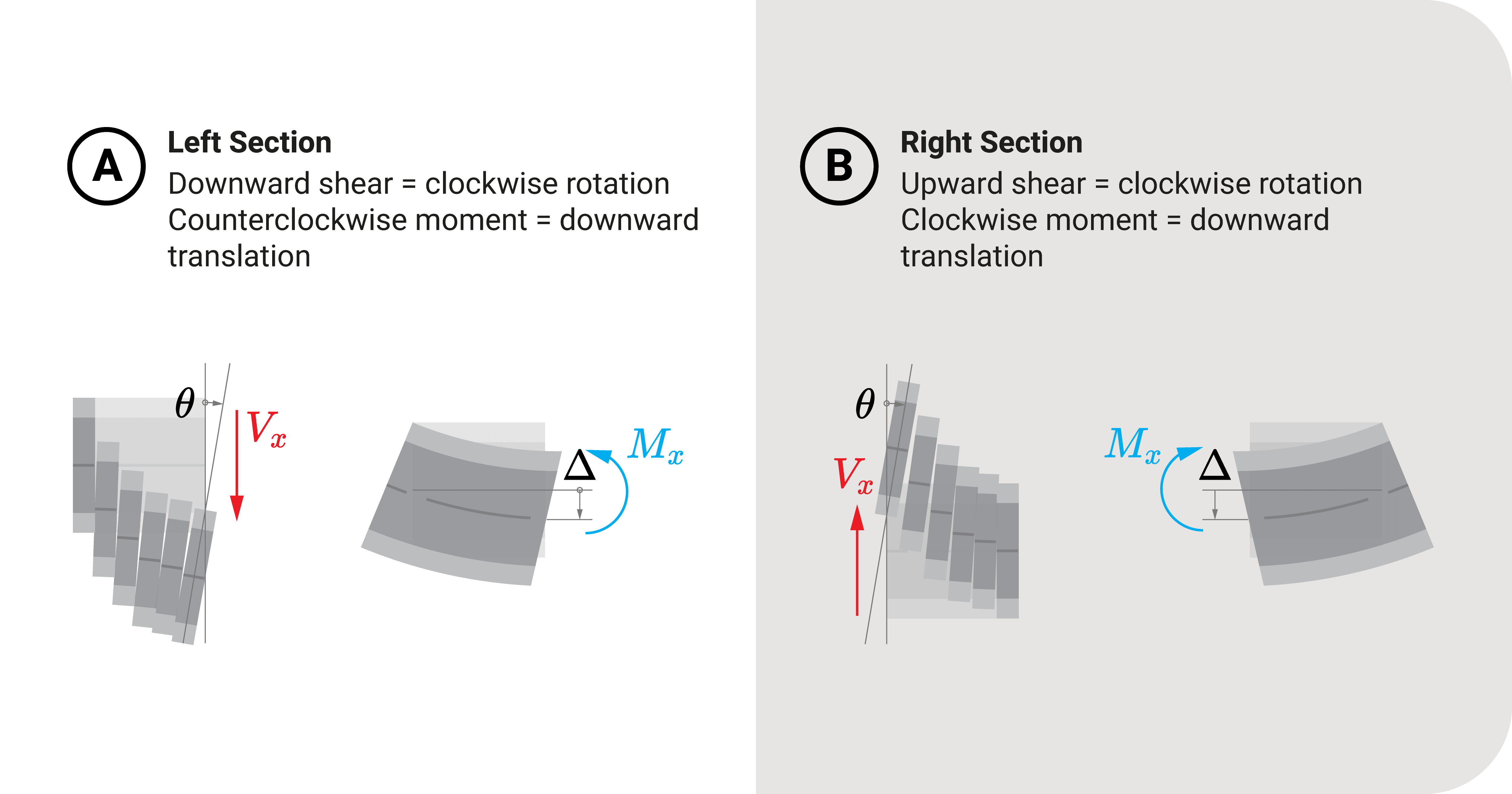
When analyzing the left section:
- If the shear is downward, the rotation is clockwise. If the shear is upward, the rotation is counterclockwise.
- If the moment is counterclockwise, then the deflections are downward. If the moment is clockwise, then the deflection is upward.
When analyzing the right section:
- If the shear is upward, the rotation is clockwise. If the shear is downward, the rotation is counterclockwise.
- If the moment is clockwise, then the deflections are downward. If the moment is counterclockwise, then the deflection is upward.
Summary
Let's summarize:
Knowing the deflection's directions will depend on the beam analysis convention.
For concaved upward convention, when analyzing the left section:
If the shear is downward, the rotation is clockwise. If the shear is upward, the rotation is counterclockwise.
If the moment is counterclockwise, then the deflections are downward. If the moment is clockwise, then the deflection is upward.
For concaved upward convention, when analyzing the right section:
If the shear is upward, the rotation is clockwise. If the shear is downward, the rotation is counterclockwise.
If the moment is clockwise, then the deflections are downward. If the moment is counterclockwise, then the deflection is upward.






