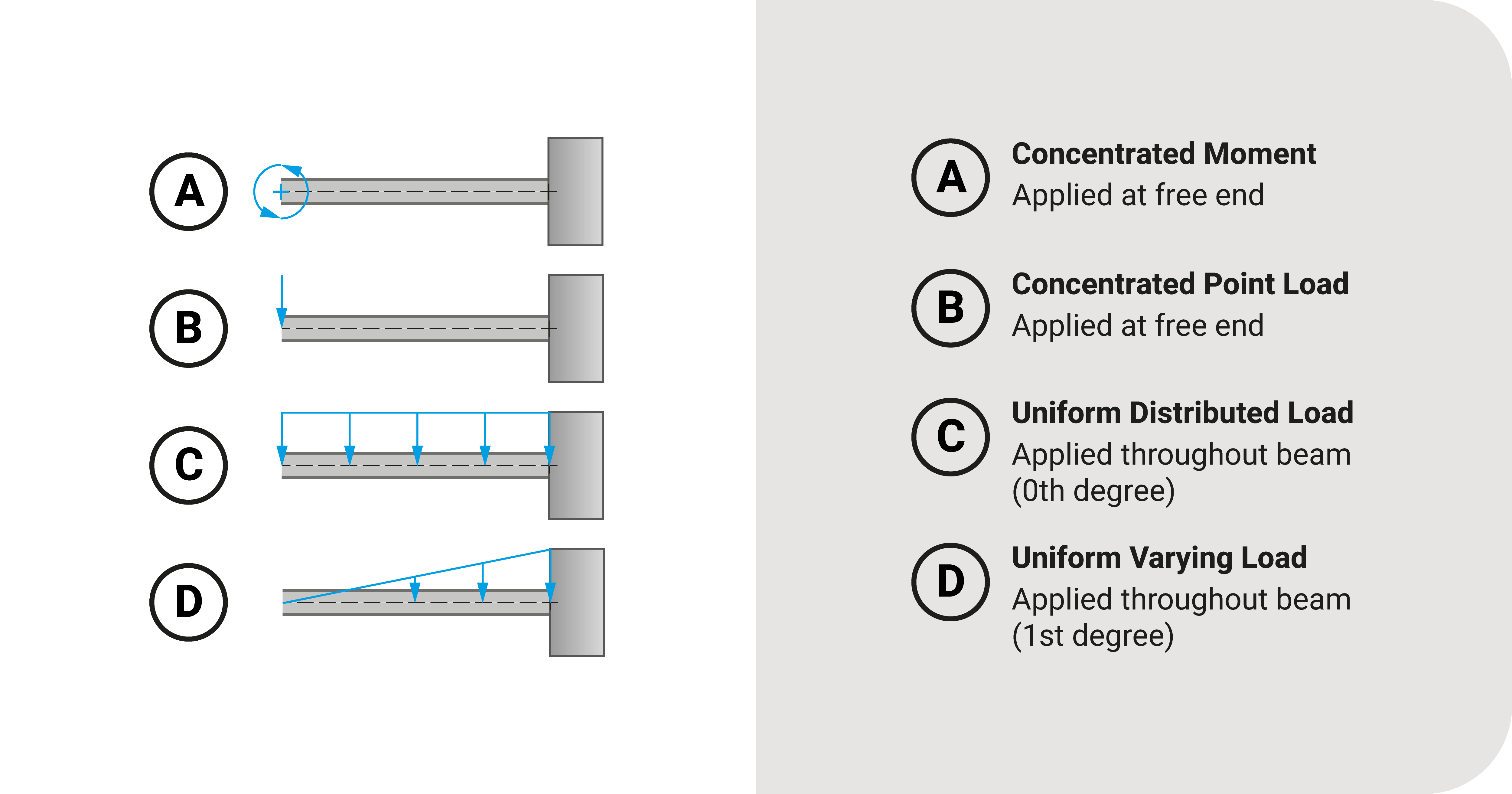
Deflection Formulas (Free-End)
We can observe an interesting pattern with the formulas of free-end deflection. Using the same loading conditions, here's a table for the rotation and translation for the series of cantilever beams:
We can create a formula that gives any rotation or translation expression in the table. It is a valuable tool rather than memorizing each equation in the table.
Rotation
Let's look at the rotation (slope) equations in the table. There is a definite pattern for these formulas:
\(\theta=\frac{XL^{i_\theta}}{N_{\theta}EI}\)
- \(X\) refers to the type of loading condition (similar to the table), which can be \(M\), \(P\), or \(w\)
- \(L\) refers to the length of the beam
- \(i_\theta\) refers to the rotation exponent
- \(N_{\theta}\) refers to the rotation denominator
- \(EI\) refers to flexural rigidity
The rotation exponent \(i_\theta\) will depend on the loading condition:
- For \(M\), \(i_\theta = 1\)
- For \(P\), \(i_\theta = 2\)
- For \(w\), \(i_\theta = 3\)
The rotation denominator \(N_{\theta}\) equals \(N!\) where \(N=(n+1)\). The variable \(n\) is the degree of the moment equation.
Example
Let's look at the loading condition for a uniform distributed load from 0 to \(L\) to demonstrate how to use the formula.
- \(X\) refers to the type of loading condition. In this case, it's \(w\).
- \(L\) refers to the length of the beam.
- \(i_\theta\) refers to the rotation exponent. In this case, it is equal to 3.
- \(N_{\theta}\) refers to the rotation denominator. It is equal to \(N!=\left(2+1\right)!=6\)
- \(EI\) refers to flexural rigidity.
From these variables, the rotation equation for the uniformly distributed load condition is: \(\frac{wL^3}{6EI}\). It is equal to the expression in the table.
Translation
Let's look at the translation equations in the table. Likewise, there is a definite pattern for these formulas:
\(\delta=\frac{XL^{i_\delta}}{N_{\delta}EI}\)
- \(X\) refers to the type of loading condition (similar to the table), which can be \(M\), \(P\), or \(w\)
- \(L\) refers to the length of the beam
- \(i_\delta\) refers to the translation exponent
- \(N_{\delta}\) refers to the translation denominator
- \(EI\) refers to flexural rigidity
The translation exponent \(i_\delta\) will depend on the loading condition:
- For \(M\), \(i_\theta = 2\)
- For \(P\), \(i_\theta = 3\)
- For \(w\), \(i_\theta = 4\)
The translation denominator \(N_{\theta}\) equals \(N!+(N-1)!\) where \(N=(n+1)\). The variable \(n\) is the degree of the moment equation.
Example
Let's look at the loading condition for a uniform distributed load from 0 to \(L\) to demonstrate how to use the formula.
- \(X\) refers to the type of loading condition. In this case, it's \(w\).
- \(L\) refers to the length of the beam.
- \(i_\delta\) refers to the translation exponent. In this case, it is equal to 4.
- \(N_{\delta}\) refers to the translation denominator. It is equal to \(N!+(N-1)!=(2+1)!+[(2+1)-1]!=8\)
- \(EI\) refers to flexural rigidity.
From these variables, the translation equation for the uniformly distributed load condition is: \(\frac{wL^4}{8EI}\). It is equal to the expression in the table.
Rotation and Translation Denominators
There is a relationship between the rotation and translation denominators, \(N_{\theta}\) and \(N_{\delta}\). To demonstrate, below are the results of \(N_{\theta}\) and \(N_{\delta}\) for each loading condition:
Starting from the first loading condition, if we add its \(N_{\theta}\) and the following subsequent load, you'll get the \(N_{\delta}\) for the next loading condition.
- The \(N_{\theta}\) of the first loading condition (a moment at free end) is 1. The \(N_{\theta}\) of the second loading condition (a point load at the free end) is 2. If we add these two values, it would be the \(N_{\delta}\) of the second loading condition, equal to 3.
This concept of adding adjacent \(N_{\theta}\) is the interpretation of \(N_{\delta}=N!+(N-1)!\)
Summary
Let's summarize:
We can observe an interesting pattern when analyzing the cantilever beam's moment and deflection.
We can observe it through a series of cantilever beams with the following loading conditions: (1) a couple at the free end, (2) concentrated point load at the free end, (3) uniform distributed load from 0 to \(L\), and (4) a uniform varying load from 0 to \(L\) (with the highest magnitude at the fixed support)
The moment equations are polynomial functions of the form \(M=kx^n\).
The moment equation's degree \(n\) is an important variable.
We can create a general formula that would give any rotation or translation expression for cantilever beams.
Rotation pattern formula is \(\theta=\frac{XL^{i_\theta}}{N_{\theta}EI}\) (see meaning of variables on post).
Translation pattern formula is \(\delta=\frac{XL^{i_\delta}}{N_{\delta}EI}\) (see meaning of variables on post).