Virtual and real work methods are essential procedures in solving translations and rotations.
Also known as energy methods, we investigate the work or energy done by the structure rather than analyzing it in terms of its loads. We then take advantage of the Law of Conservation of Energy to solve for the deflections.
One massive benefit of the work methods is that they allow you to solve for the deflection of plane beams, frames, and trusses.
Preparation
This post serves as a preparation stage. We will need to understand several topics to understand the work methods.
- Work and Energy
- Law of Conservation of Energy
- Strain Energy
- Superposition
Work, Energy, and the Law of Conservation of Energy
- Work \(W\) happens if a force or moment causes something to move: \(W=P{\times}{\Delta}\) or \(W=M{\times}{\theta}\).
- Energy is the ability to do work.
- The Law of Conservation of Energy states that nothing can create or destroy energy.
You can learn more about these concepts in this post.
Relating Work and Energy
Work and energy can be related using the Law of Conservation of Energy. Concerning our topic of structural deflections, we'll consider a beam example.
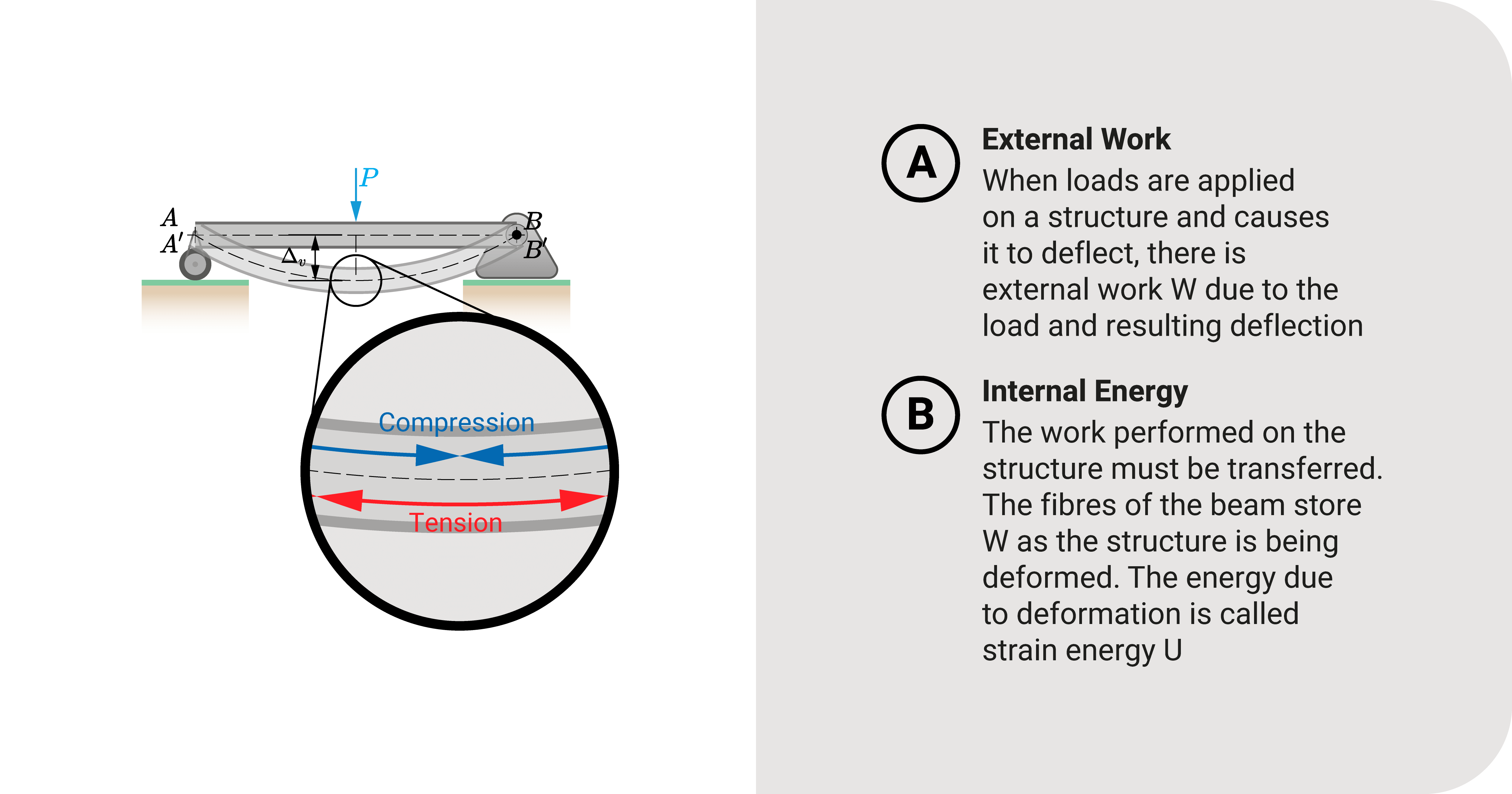
When loads apply to it and cause deflection, there is external work \(W\). From the law of conservation of energy, this external work \(W\) has to transfer somewhere. As the beam deflects from its original position, the fibers of the beam will deform and store the external work \(W\) in the form of strain energy \(U\). Generally speaking, we can express this law for this system as:
\(W=U\)
Strain Energy
Let's expound on strain energy \(U\). Formally, this is potential energy due to the deformation of an object.
To illustrate what it is, say that we have a fixed bar on one end, as seen in the figure. Initially, this bar is unstressed and experiences no form of load. When we apply a tension force \(P\) on the free end, the bar elongates by \(\Delta\), and there is external work \(W\). It causes the bar to experience axial strains in the form of strain energy \(U\). When we remove tension force, the bar may or may not return to its original state depending on its properties.
With \(U\), the next question is: how do we compute strain energy \(U\)? The answer to that question will depend on the amount of \(P\) applied and the object's deformation.



.png)







