We now move on to solving deflections using real work. Unlike virtual work involving a fictional load, we'll use actual forces and displacements to find translations and rotations.
Generally, there are two approaches: (1) general real work and (2) Castigliano's second theorem.
Setting Up the General Real Work Equation
Say we have a simple beam \(AB\) loaded with a point load \(F\) at point \(C\). We want to investigate the translation at \(C\).
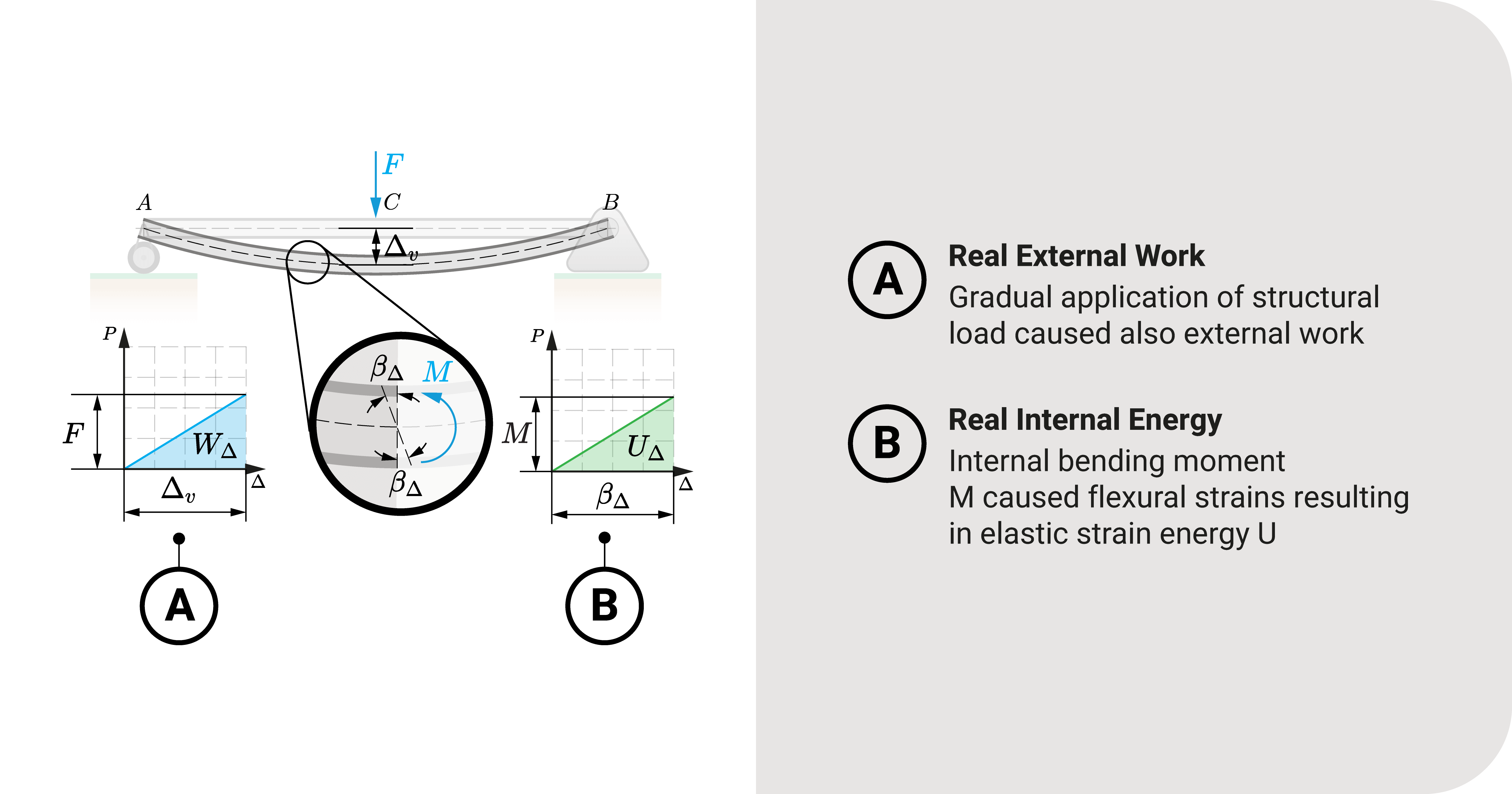
From energy conservation, when there is an applied load \(F\) that caused \(\Delta\), there is total external work \(W\) and strain energy \(U\):
Equation 1: \(W=U\)
In this situation, we'll assume that F was applied gradually, as seen in the \(P-\Delta\) graph in the figure. It makes the structure behave within the elastic region.
The total external work \(W\) is then equal to:
Equation 2: \(W=\frac{1}{2}F\Delta_v\)
Key Idea: General Real Work Equation
We equate Equations 1 and 2 to formulate the general equation used to find deflections using real work:
General Equation of Real Work - Translation: \(\frac{1}{2}\times{F}\times{\Delta}=U\)
General Equation of Real Work - Rotation: \(\frac{1}{2}\times{M}\times{\theta}=U\)
- \(F\) (or \(M\)) refers to the actual load (or couple) at position x.
- \(\Delta\) (or \(\theta\)) refers to the deflection we would like to investigate at the point where \(F\) (or \(M\)) is located (at position \(x\)).
- \(U\) is strain energy.
Limitation
If we compare these with the virtual work general equation, these equations are more straightforward. However, one drawback is that you can solve only one deflection component where the point load or couple is applied. It implies that this method is minimal, making the virtual work method seem more advantageous.
To explain, for our beam example, you can only solve for the vertical translation at \(C\) (and only at that point) because force \(F\) is at \(C\). For other locations where \(F\) or \(M\) is not directly applied, we will be using another theorem later on.
Real Strain Energy
We need to expound on the general real work equation due to strain energy \(U\) (similar to what we did with the general virtual work equation). This value would entirely depend on the primary stress the structure is experiencing, whether flexural, axial, or torsional.
Summary
Let's summarize:
Real work uses actual forces and displacements to find translations and rotations.
The general equation for real work are \(\frac{1}{2}\times{F}\times{\Delta}=U\) and \(\frac{1}{2}\times{M}\times{\theta}=U\)
One drawback is that you can solve only one deflection component where the point load or couple is applied.
We need to expound on the general real work equation due to strain energy \(U\). This value would entirely depend on the primary stress the structure is experiencing, whether flexural, axial, or torsional.





.png)

