Let's learn how to use the real work method to solve deflections. This example presents a case of axial strains.
The solution presented is in SI. The author will update the post soon to reflect English units.
To start, we shall consider a simple truss. It has a \(20 kN\) point load at \(E\). The value inside the parenthesis () is the member's cross-sectional area \(A\) in square centimeters.
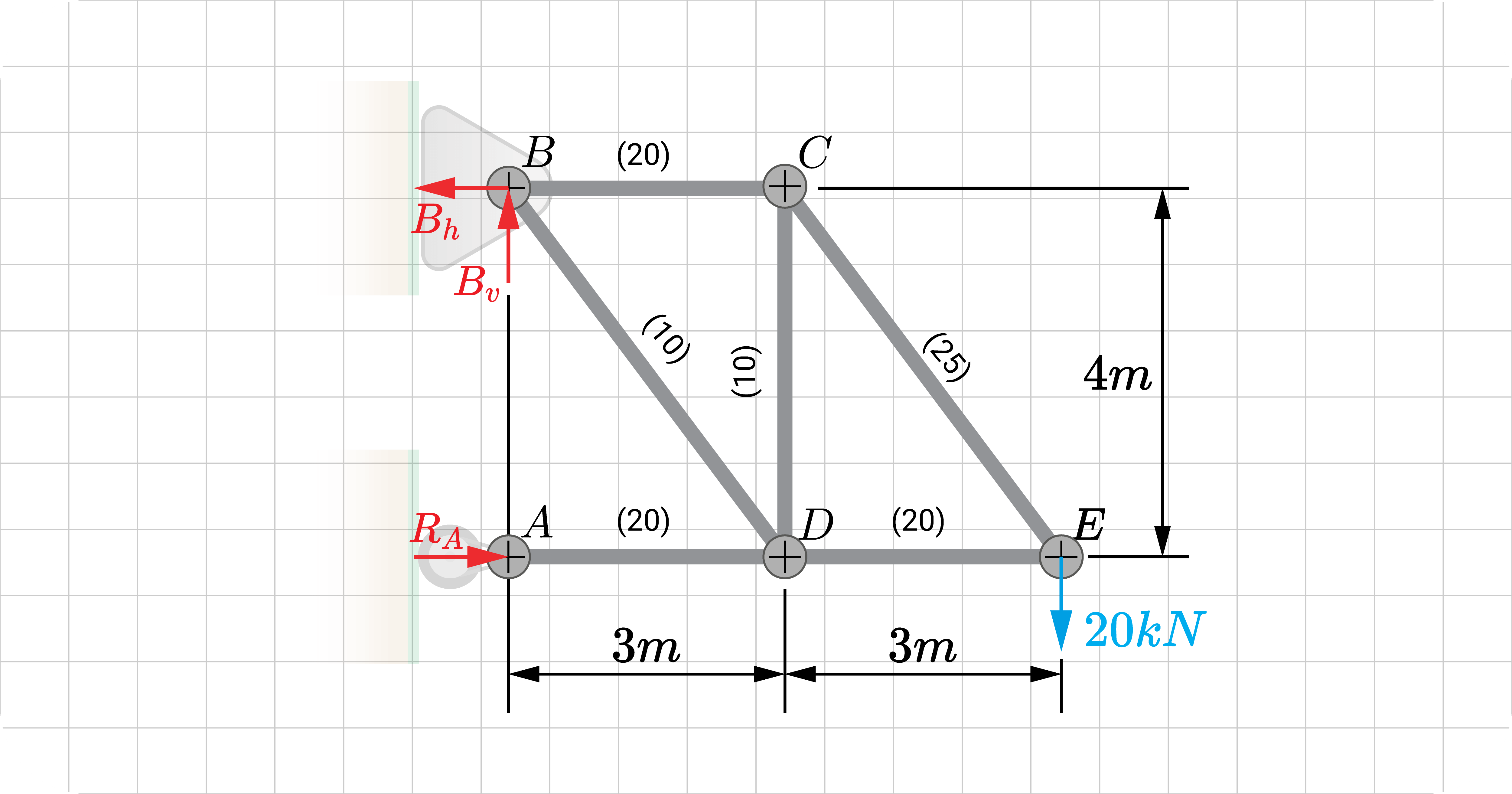
Say that we are interested in finding the vertical translation \(\Delta_{E_v}\) at \(E\). Because there is a point load at said point, we solve for the vertical deflection using the general real work equation. We can use it on other points if there's a load.
For this problem, we'll assume that all members are made of the same material so that the modulus of elasticity \(E\) is constant.





