This post introduces the first theorem of the area moment method: change in slope.
Deriving Change in Slope
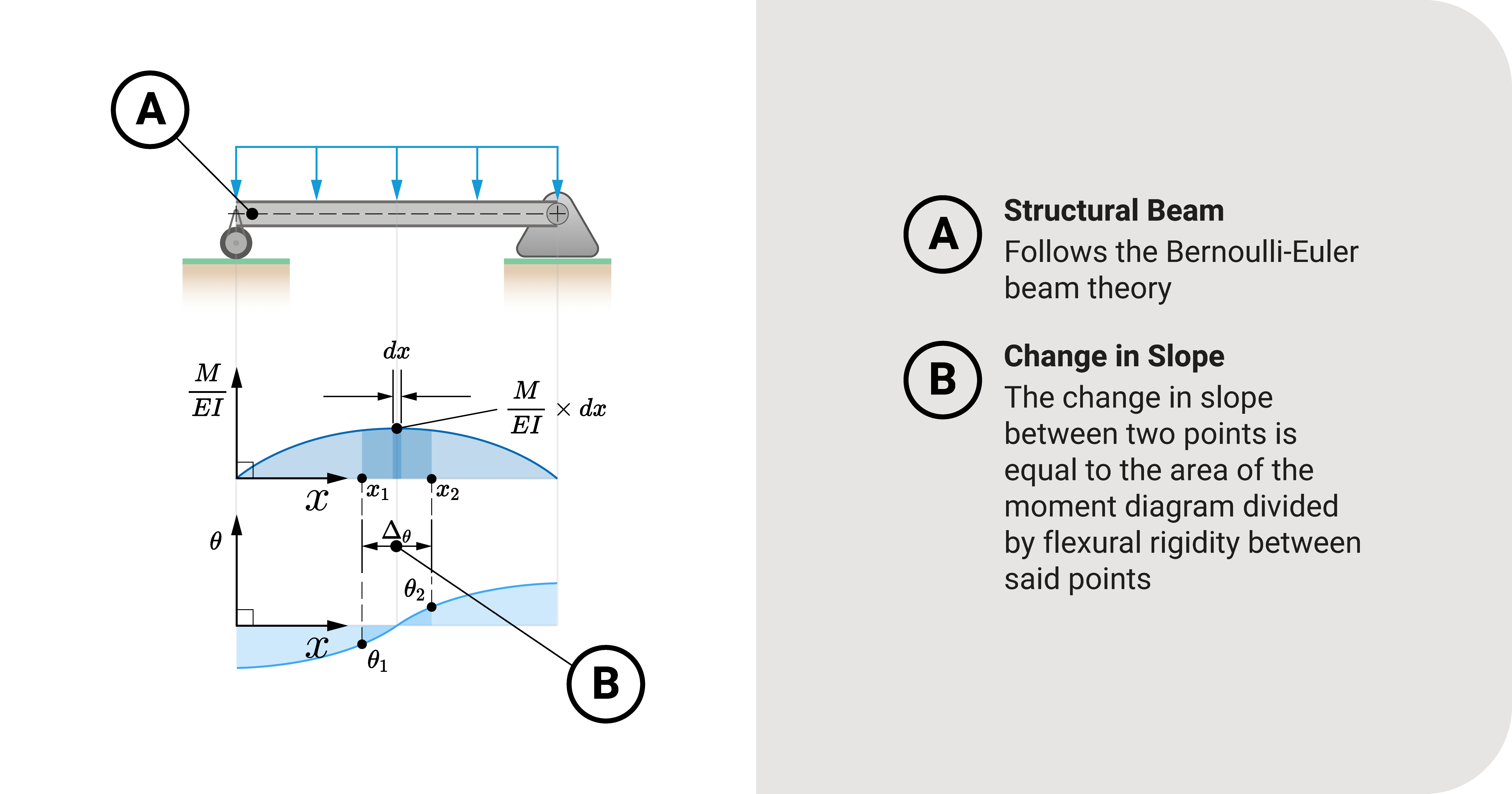
There are many ways to derive the first theorem. We first start by recalling the Bernoulli-Euler Beam Equation.
\(\frac{d^2\Delta}{dx^2}=\frac{M}{EI}\)
If you integrate this equation once, it will lead you to an expression describing the slope of the deflected shape:
\(\frac{d\Delta}{dx}=\theta=\int\frac{M}{EI}dx\)
In Calculus, if you integrate an equation, you a the area between curves. So, if you evaluate the integral of \(\frac{M}{EI}\) from position \(x_1\) to \(x_2\), then you are getting the area or the change of slope between these two positions.
\(\Delta_\theta=\theta_2-\theta_1=\int_{x_1}^{x_2}\frac{M}{EI}dx\)
This expression is the first theorem of the area moment method: "the change in slope between two points \(x_1\) and \(x_2\) is equal to the area of the \(\frac{M}{EI}\) diagram between said points."
Another way of saying this is that if you get the area between two points of the moment against the structure's rigidity diagram, you'll be getting the difference in slope between said points.
Sign Convention
We have to pay attention to the meaning of the sign. It can tell us if the angular deflection is clockwise or counterclockwise from a reference:
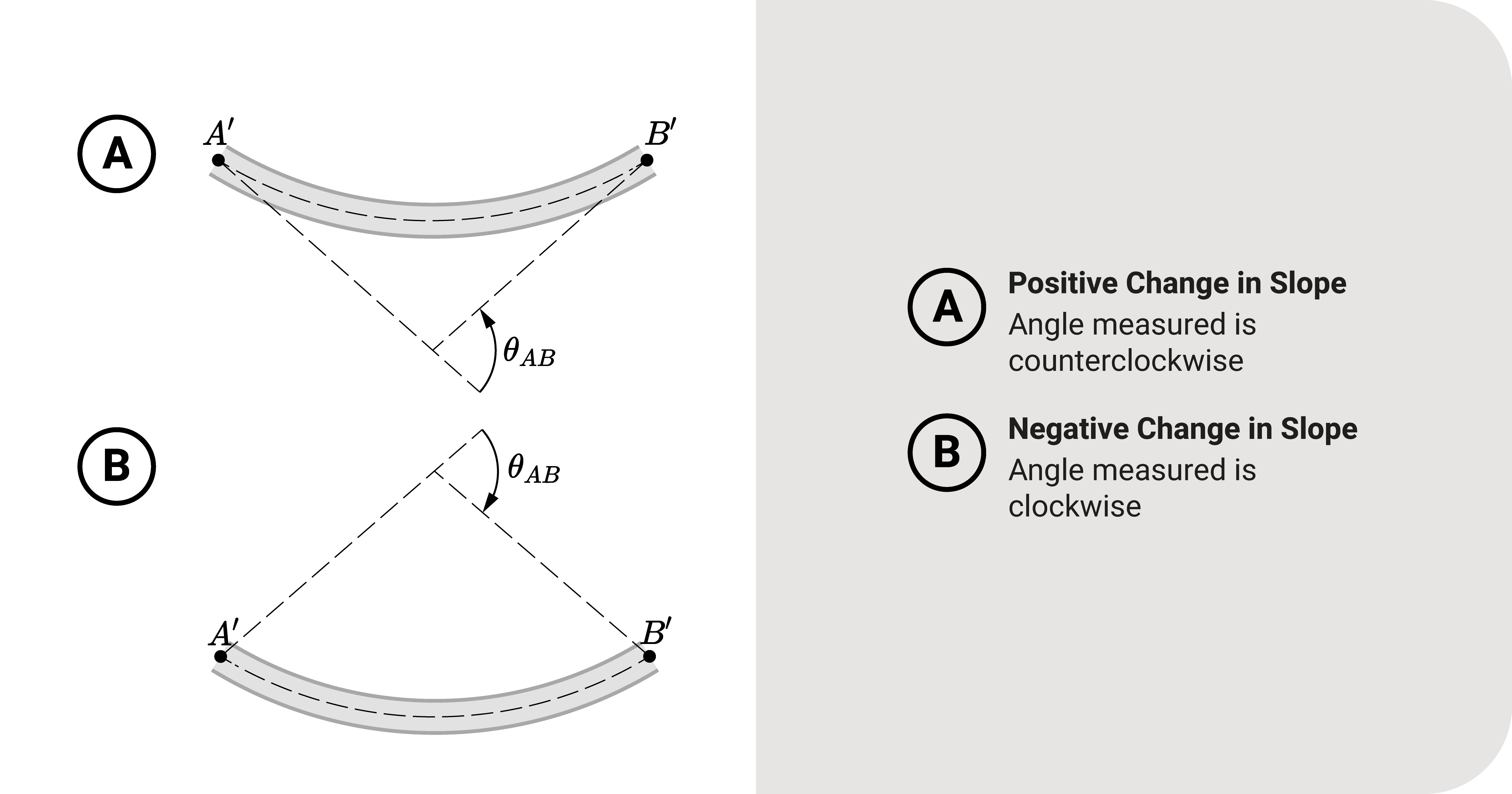
- Positive rotation means the direction is counterclockwise.
- Negative means it is clockwise.
Summary
Let's summarize:
The first theorem states that "the change in slope between two points \(x_1\) and \(x_2\) is equal to the area of the \(\frac{M}{EI}\) diagram between said points."
\(\Delta_\theta=\theta_2-\theta_1=\int_{x_1}^{x_2}\frac{M}{EI}dx\)
In sign convention, positive rotation means the direction is counterclockwise, while negative is clockwise.





