Another differential equation (DE) application is Newton's Law of Cooling. Sir Isaac Newton was interested in quantitatively finding the heat loss in an object; hence, he derived a model that would represent this event.
Modeling Newton's Law of Cooling
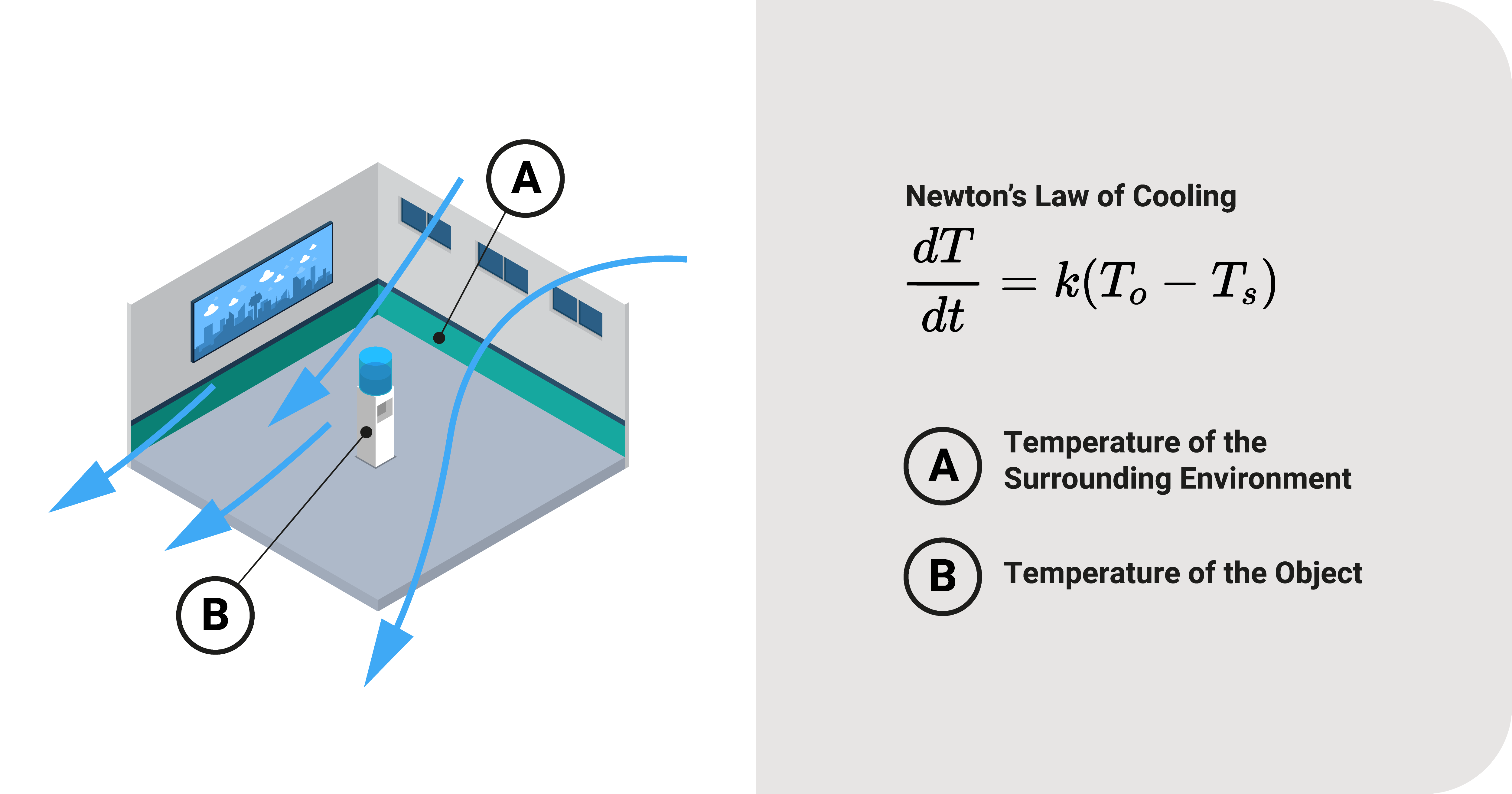
Consider an object in space like a cup of hot water in a cold room. From thermodynamics, we know that this hot water will eventually cool off. How fast this water cools over a period \(\frac{dT}{dt}\) is proportional to the difference between the temperature of the object \(T_o\) and its surroundings \(T_s\). Representing it using equations, we have:
- \(\frac{dT}{dt} \propto T_o-T_s\)
- \(\frac{dT}{dt} = k(T_o-T_s)\), where \(k\) is the constant of proportionality
We can solve this DE using the separation of variables technique and expressing the solution in its exponential form:
- \(\frac{dT}{dt} = k(T_o-T_s)\)
- \(\frac{dT}{T_o-T_s} = k \cdot dt\)
- \(\ln (T_o-T_s)=kt + \ln C\)
- \(\ln (T_o-T_s)-\ln C=kt\)
- \(\ln \frac{T_o-T_s}{C}=kt\)
- \(e^{\ln \frac{T_o-T_s}{C}}=e^{kt}\)
- \(\frac{T_o-T_s}{C}=e^{kt}\)
- \(T_o=Ce^{kt}+T_s\)
This equation, \(T_o=Ce^{kt}+T_s\), is Newton's Law of Cooling. It consists of the following constants and variables:
- \(C\) is the initial value
- \(k\) is the constant of proportionality
- \(t\) is time
- \(T_o\) is temperature of the object at time \(t\)
- \(T_s\) is the constant temperature of the surrounding environment.






