What is the Logistic Differential Equation?

Modeling Logistics

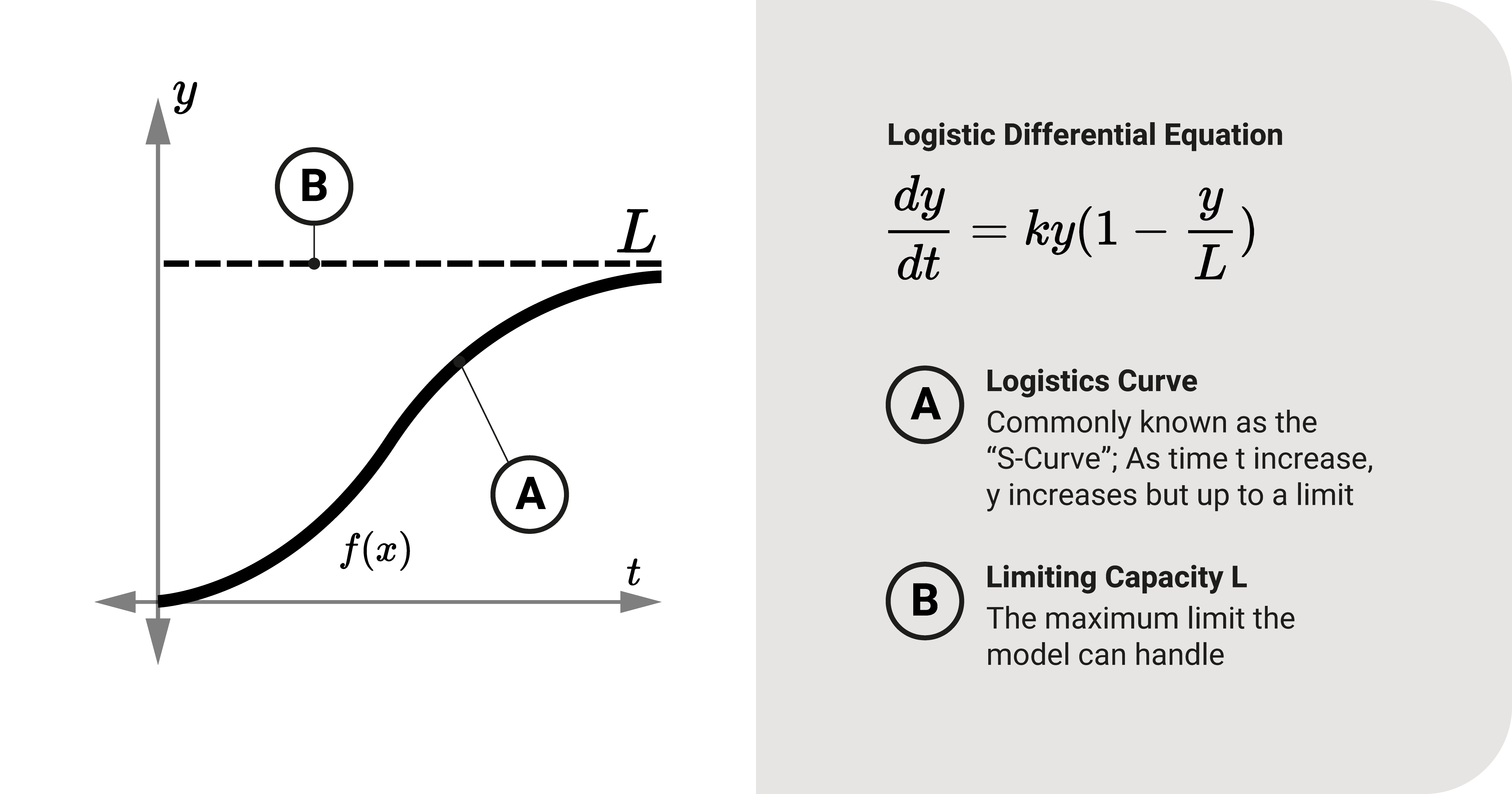
Let's recall that for some phenomena, the rate of change is directly proportional to its quantity, just like we did with growth and decay; However, this is only sometimes the case. To illustrate, let's look at population growth. We can model it exponentially as $y=C{e}^{kt}$, but this assumes that the population will grow infinitely.

As time passes, population growth decreases because of a specific limitation $L$. It happens due to a lot of factors. In our example, the growth slowed down probably because the place has limited resources to offer its people; hence, people leave the area. As a consequence, it regulates growth.

It may be best to model these events using the logistic differential equation. Pierre François Verhulst, a Belgian Mathematician, first created this equation. It states that the rate of change is directly proportional to the difference between quantity $y$ and a limiting term $\frac{y^2}{L}$:

• $\frac{dy}{dt}\propto (y-\frac{y^2}{L})$
• $\frac{dy}{dt}\propto y(1-\frac{y}{L})$
• $\frac{dy}{dt}=ky(1-\frac{y}{L})$

The model grows at a $k$ growth rate as time $t$ goes by. At some point, $y$ would approach a limiting capacity $L$.

We can find the general solution using the separation of variables method or Bernoulli's Equation. Let's use the latter:

• $\frac{dy}{dt}=ky(1-\frac{y}{L})$

Rearranging the form:

• $\frac{dy}{dt}-ky=-\frac{k{y}^2}{L}$

Applying Bernoulli's Equation:

• $y^{\prime }{y}^{-2}-k{y}^{-1}=-\frac{k}{L}$, eliminate $y^n$
• $\frac{d\left(y^{-1}\right)}{dt}+k{y}^{-1}=\frac{k}{L}$, make first term conform to standard form
• $\frac{dz}{dt}+kz=\frac{k}{L}$, let $y^m$ be $z$ and solve for $z$
• $\mu =e^{\int kdt}=e^{kt}$, solve for integrating factor
• $z=\frac{1}{e^{kt}}\int \frac{k}{L}{e}^{kt}dt$, solve for general solution
• $z=\frac{1}{e^{kt}L}(e^{kt}+C_1)=y^{-1}$
• $y=\frac{e^{kt}L}{e^{kt}+C_1}$
• $y=\frac{L}{1+C{e}^{-kt}}$

The general solution is what we call the logistic function, which consists of the following:

• $L$ is the limiting capacity
• $C$ is the initial value
• $k$ is the growth rate
• $t$ is time

We can view the solution curve graphically in the figure. It looks like a sigmoid curve (commonly known as the "S-Curve"). It has a horizontal asymptote at $y=L$, which would satisfy the model's limiting condition $L$.